Статья 2.

Теорема о шести окружностях или теорема о четырех пучках.
Пучки окружностей, их определение, виды и свойства.

Краткое содержание.

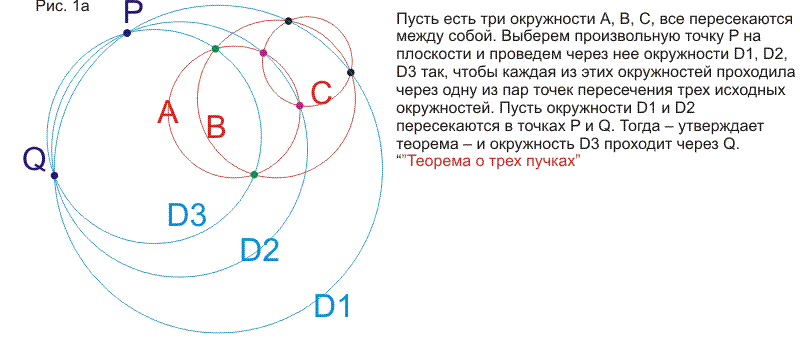
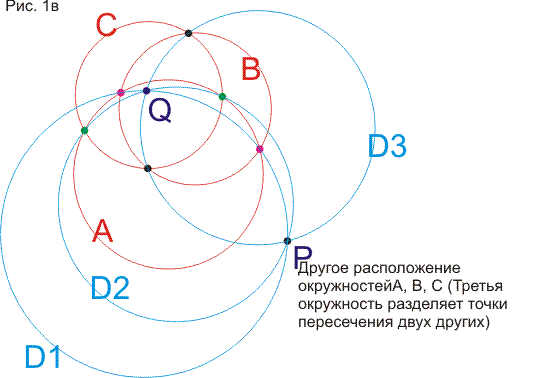
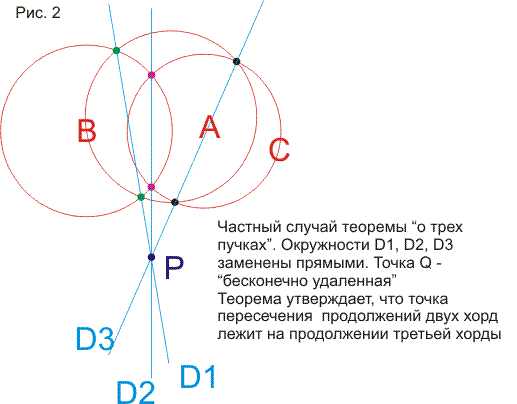
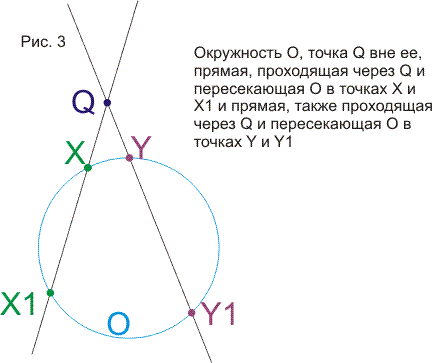
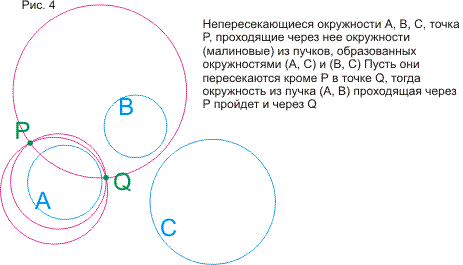
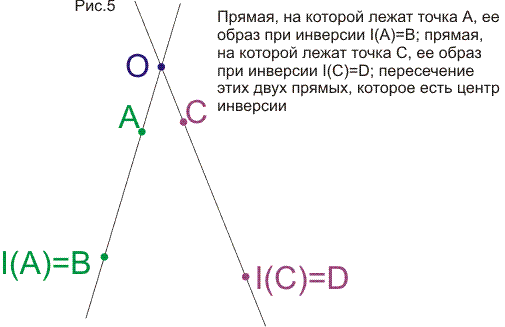
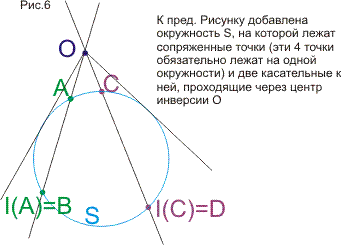
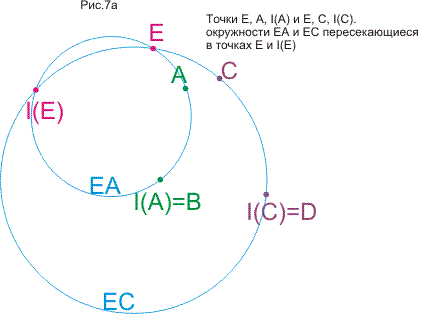
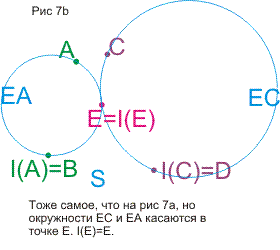
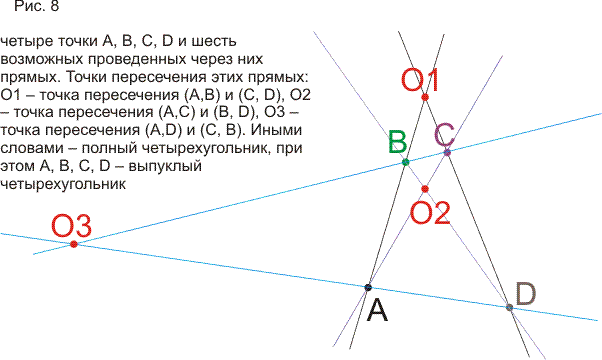
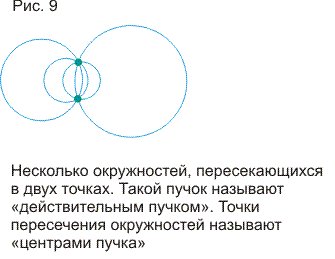
Сначала здесь рассматривается теорем о шести окружностях или теорема о четырех пучках. После вычислительного, "школьного" доказательства приводятся доказательства, использующие простые объемные построения. Становится ясным, что теорема обобщается и на многомерные пространства и в плоском варианте. Затем решается задача о нахождении образа точки Х при какой-то инверсии I, если не известна окружность инверсии, но известны образы двух других точек при этой инверсии. Задача неожиданно приводит нас снова к теореме о шести окружностях. Затем определяются "пучки" окружностей (они появляются при обобщении теоремы о шести окружностях) и рассматриваются их свойства. В конце статьи рассматриваются симметрии относительно точек и прямых в контексте геометрии окружности и используются элементы теории групп (без явных определений и от читателя не требуются предварительные знания).

Формулировка теоремы.






Исключение. Возможно, что D1 и D2 касаются друг друга в точке Р. Тогда теорема утверждает, что и D3 касается их в точке Р.

Стандартное или школьное доказательство.


Обыкновенно задачу про окружности стараются свести к задачам про прямые, лучше всего – перпендикулярные (а еще лучше – к векторам) и подсчитать какие-нибудь углы и расстояния. В данном случае доказательство использует одну важную идею: если условие задачи содержит только слова "точка" и "окружность" и требуется доказать, что какие-то точки лежат на одной окружности (или окружности пересекаются в одной точке) то можно провести инверсию относительно любой окружности и решать задачу уже про инвертированные точки и окружности. Ведь при инверсии – окружности перейдут в окружности, а точки пересечения – в точки пересечения инвертированных окружностей. Если выбрать центр инверсии в точке пересечения каких-то окружностей, то эти окружности перейдут в прямые. А теоремы о прямых "школьная" геометрия умеет доказывать.
Осуществим инверсию с центром в точке Р. Тогда окружности D1, D2, D3 перейдут в прямые, т.к. по условию проходят через Р, центр инверсии. Нарисуем результат инверсии.


Прямые D1, D2, D3 имеют общую бесконечно удаленную точку. Это – образ точки Р при инверсии. Требуется доказать, что все они пересекаются в одной точке Q. Пусть АВ1 и АВ2; ВС1 и ВС2; АС1 и АС2 – точки пересечения соответственных окружностей. Проведем две прямые D2 и D3 – они пересекутся в точке Q, достаточно доказать, что прямая, проходящая через Q и АС1 проходит и через АС2. Для этого воспользуемся свойством секущих к окружности.


Свойство связывает расстояния: |Q,X|*|Q,X1|=|Q,Y|*|Q,Y1| тогда и только тогда, когда X, X1, Y, Y1 лежат на одной окружности ("только когда" требует уточнения, о том, что Q – не разделяет пары точек пересечения Х, Х1; и Y, Y1. Причем если Q лежит внутри окружности, то напротив, необходимо чтобы Q разделяла точки пересечения, а формула останется неизменной).
Применим это свойство к рисунку 2.
|Q, AB1|*|Q,AB2|=|Q,BC1|*|Q,BC2| т.к. все эти точки лежат на окружности В. Пусть Х – вторая точка пересечения прямой (Q, АС1) с окружностью С, надо доказать, что она лежит на окружности А. Отсюда сразу следует, что она и есть АС2. |Q,AC1|*|Q,X|=|Q, BС1|*|Q, BС2| т.к. AC1, BС1, BС2 и Х – на окружности С. Но, как было уже сказано |Q, AB1|*|Q,AB2|=|Q,BC1|*|Q,BC2|, значит |Q, AB1|*|Q,AB2|=|Q,AC1|*|Q,X| АВ1, АВ2, АС1 – лежат на А, значит по свойству длин секущих – и Х лежит на А, по построению Х лежит и на С, значит Х – вторая точка пересечения А и С, что и требовалось. Заметим, что если бы окружность С разделяла точки пересечения А и В, то, после инверсии Q разделяла бы точки АС1 и АС2 и другие точки пересечения. Доказательство в этом случае было бы аналогично. Это – хорошее доказательство, но оно проходит мимо разных случаев обобщения этой теоремы.

Второе доказательство.

Оно использует объемные построения и избавляет нас от подсчета каких-либо расстояний. Будем мыслить окружности проведенными на сфере. При этом все теоремы геометрии окружности будут точно такими же. Окружность на сфере – это линия пересечения сферы с плоскостью. Поэтому каждая окружность на сфере задает плоскость в пространстве (ту, на которой лежит). Обратное не верно: плоскость, не имеющая со сферой общих точек не задает никакой окружности. Правда, такая плоскость задает отображение сферы в себя (симметрию), которая, как и инверсия – отображает окружности в окружности, сохраняет углы между окружностями и т.п. Но у этого отображения – нет неподвижных точек, в отличие от обычной инверсии. Это – мнимая инверсия. Если две окружности пересекаются, то их плоскости пересекаются по прямой, проходящей через сферу и точки пересечения этой прямой со сферой есть точки пересечения двух окружностей. Каждой плоскости, проходящей через эту прямую, отвечает окружность на сфере, проходящая через эти две точки (точки пересечения прямой и плоскости). Можно сказать, что всякой прямой, пересекающей сферу соответствуют окружности, проходящие через точки пересечения ее со сферой. Что будет, если прямая касается сферы? В этом случае плоскости, проходящие через данную прямую, пересекаются со сферой по окружностям, касающимися этой прямой и друг друга в точке касания прямой и сферы. Если прямая не имеет со сферой общих точек, то некоторые плоскости, проходящие через нее, пересекаются со сферой, две плоскости – касаются со сферой, а другие проходят мимо сферы. Получающееся семейство окружностей (по которым плоскости, проходящие через данную прямую пересекают сферу) не пересекаются друг с другом, все окружности лежат одна внутри другой и обладают рядом свойств, схожими с предыдущими двумя случаями. Это семейство окружностей называют "пучком окружностей". Теперь докажем теорему.
Вернемся к рис. 1 Рассмотрим окружности А, В, D1 и D3. Нам известно, по условию, что все эти окружности пересекаются между собой, и что точки пересечения D1 с А и D3 с В лежат на одной окружности (это окружность С). Требуется доказать, что точки пересечения А и В лежат на одной окружности с точками пересечения D1 и D3 (именно через них проходит, точнее, должна проходить по теореме окружность D2). Перейдем к плоскостям, в которых лежат окружности A, B, D1 и D3. Тот факт, что точки пересечения А с В и D1 с D3 лежат на одной окружности эквивалентен тому, что эти четыре точки лежат на одной плоскости. Пусть теперь А, В, D1 и D3 означают не только окружности, но и плоскости, в которых они лежат (что именно, окружности или плоскости – будет ясно из контекста). Пересечение А с D1 – прямая, и В с D3 – прямая. Эти две прямые лежат в одной плоскости (в которой лежит окружность С). Требуется доказать, что пересечение А с В и D1 c D3 – также лежат в одной плоскости. Докажем от противного. Если А∩В и D1∩D3 не лежат в одной плоскости, то они не пересекаются, следовательно пересечение А∩В∩D1∩D3 – пусто. Но по условию А∩D1 и В∩D3 – в одной плоскости, следовательно эти прямые имеют общую точку (считаем параллельные прямые пересекающимися бесконечно далеко). Следовательно пересечение А∩В∩D1∩D3 не пусто. Противоречие, что и требовалось доказать.
Немного терпения. Еще раз переформулируем теорему. Назовем пучком плоскостей семейство плоскостей, проходящих через какую-то одну прямую. Назовем пучки плоскостей соединимыми, если существует плоскость, лежащая в двух этих пучках одновременно. Это равносильно тому, что две прямые, образующие два этих пучка – лежат в одной плоскости. Пусть как и ранее, А, В, D1, D3 – произвольные плоскости. Четыре плоскости можно разбить на пары тремя способами.
1. (А, В) и (D1, D3)
2. (A, D1) и (B, D3)
3. (A, D3) и (B, D1)
Мы только что доказали, что если в каком-то случае пучки соединимы (т.е. пересечения пар плоскостей сами лежат в одной плоскости), то и остальные пары пучков – соединимы. Обозначим это утверждение (*). Доказательство, как мы видели, сводилось к тому, что соединимость двух пучков равносильна тому, что пары плоскостей, образующих пучки – пересекаются в одной точке). В нашем случае имеется предусмотренное пунктом 2. Мы доказали что из этого следует 1. и 3.
Теперь перейдем к окружностям на сфере. Для этого рассмотрим какую-то сферу, пересекающую все четыре плоскости. Мы доказали более общее утверждение. Например, пусть окружности А, В, С – не пересекаются.


Заметим, что пока мы не разобрали, как построить на плоскости окружность, проходящую через данную точку и данный пучок.
Теперь, как и было обещано в начале, обобщим теорему.
Изменим, обозначения. Пусть А, В, С, D – гиперплоскости. Точно также определим пучок гиперплоскостей, как совокупность гиперплоскостей таких, что пересечение любых двух совпадает (это будет гиперплоскость размерности на 1 меньше, чем у исходных). Назовем два пучка соединимыми, если есть гиперплоскость, лежащая сразу в двух этих пучках. Тогда соединимость пучка, заданного например, парой А и В с пучком, заданным парой С и D равносильна тому, что А∩В∩С∩D есть гиперплоскость размерности на 2 меньше чем у А, В, С, D (а в общем случае было бы на три меньше). И имеет место утверждение (*). поместим в это многомерное пространство гиперсферу. Гиперплоскости пересекут ее по гиперокружностям. Точно также можно определить пучки гиперокружностей и получить теорему: если пучки гиперокружностей (А, В) и (С, Д) – соединимы то (А, С) и (В, D) – соединимы и (A, D) с (В, С) – соединимы.

Третье доказательство.


Его достоинства: оно короткое; оно использует только свойства окружностей и сфер, а не свойства плоскостей, прямых и расстояний; решение плоской задачи использует объемные построения.
Представим себе, что все построение исходной задачи расположено не на одной плоскости (сфере) а выполнено в трехмерном пространстве. Легко показать, что если окружности А, В, С пересекаются между собой в разных точках, то они все лежат на одной сфере. Это будет сделано в статье 3, а здесь, ради экономии места не будем отвлекаться. Пусть точка Р лежит вне этой сферы. Проведем сферы SA через P и А, SВ через Р и В, SС через Р и С. (если Р лежит на той же сфере, что и А, В, С, то SA=SB=SC и доказательство не проходит)
Эти три сферы в общем случае пересекаются в двух точках. Одна из этих точек – Р (по построению они все проходят через нее). Обозначим вторую за Q. Покажем, что три окружности, проходящие через точку Р и точки пересечения А∩В, В∩С, С∩А – проходят через Q. Пересечение SA и SB проходит через P и А∩В также SB∩SC – через P и В∩С, SA∩SC – через Р и А∩С. Это и есть те три окружности, проходящие через Р и точки пересечения А, В и С между собой. Пересечение трех этих окружностей есть SA∩SB∩SC – это есть две точки Р и Q, следовательно три эти окружности проходят через P и Q. что и требовалось. Случай, когда сферы SA, SB, SC имеют лишь одну общую точку означает, что рассматриваемые окружности – все касаются друг друга. Мы не будем здесь это рассматривать, хотя это и не сложно. Заметим, что это доказательство также можно обобщить на пространства высших размерностей.

Снова про инверсии.


Теперь займемся задачей на первый взгляд не связанной с рассмотренной ранее теоремой.
Инверсию обычно определяют, задавая окружность (относительно которой осуществляется инверсия). А если мы знаем образы и прообразы нескольких точек (иначе говоря – пары сопряженных точек) – как определить инверсию, сопрягающие эти точки? Или, если мы знаем что I(A)=B, I(C)=D и нам дана некая точка Е, то как определить с какой точкой она сопряжена относительно I? Как должны быть связаны между собой эти пары точек, если известно, что существует инверсия I, такая, что I(A)=B, I(C)=D?
По определению инверсии, центр инверсии, образ и прообраз точки – всегда лежат на одной прямой.


(Прямая, на которой лежат точка А, ее образ при инверсии I(A)=B; прямая, на которой лежат точка С, ее образ при инверсии I(C)=D; пересечение этих двух прямых, которое есть центр инверсии)
Пусть О – центр инверсии, лежащий на пересечении прямых (А, I(A)) и (С, I(C)) (если эти прямые параллельны, то мы имеем дело с симметрией относительно прямой. Радиус инверсии можно определить из формулы: |O, A|*|O, I(A)|=R*R или |O, B|*|O, I(B)|=R*R. Из этих же формул мы извлекаем равенство: |O, A|*|O, I(A)|= |O, B|*|O, I(B)| Отсюда следует, что точки А, I(A)=B, C, I(C)=D лежат на одной окружности. (то, что две пары сопряженных точек лежат на одной окружности мы доказали иным способом в статье 1, рассматривая ортогональные окружности).
Построим теперь окружность инверсии.


Окружность с центром в О и проходящая через точки касания S с проходящими через О касательными к S и будет искомой. Ее радиус в квадрате будет равен произведению длин: |O, A|*|O, I(A)|=|O, B|*|O, I(B)| (По теореме о секущих к окружности). Но нам интересна сейчас не столько сама окружность инверсии, а построение образа какой-то точки Е, если даны А, I(A); C, I(C). I(E)=?
Проведем окружность ЕА через Е, А, I(A). Т.к. она проходит через пару сопряженных относительно I точек, то она ортогональна I и I(EA)=EA и точка I(E) – лежит на ней. Аналогично проведем окружность ЕС через E, C, I(C) по той же причине она переходит в себя при инверсии относительно I, I(EC)=EC. Значит I(E) лежит на ЕС. Значит – I(E) – есть вторая точка пересечения окружностей ЕС и ЕА (их первая точка пересечения – это Е). Если же ЕА и ЕС касаются, то I(E)=E.




Итак, мы научились проведением всего двух окружностей находить образ произвольной точки Е, если известны образы точек А и С. Но возникает один вопрос. Возьмем какую-нибудь точку К. I(К) можно найти исходя из двух пар сопряженных точек: А, I(A) и C, I(C). Но мы уже построили еще одну пару сопряженных точек: Е, I(E). Если мы найдем I(K) c помощью пар сопряженных точек А, I(A) и E, I(E) – получим ли мы ту же самую точку?
Проведем окружности:
S1 через A, I(A), C, I(C); S2 через С, I(С), Е, I(Е); S3 через A, I(A), Е, I(Е). Теперь проведем еще три окружности: К1 через К, А, I(A); К2 через К, С, I(С); К3 через К, Е, I(Е). по доказанной теореме о шести окружностях – все они пересекаются в одной точке, эта точка и будет I(E). Это и доказывает, что I(E) не зависит от того, с помощью каких пар сопряженных относительно I точек его находить. Заметим, что поскольку нам известно, что I(E) – существует и единственно, мы можем таким образом получить новое, четвертое доказательство теоремы о шести окружностях.
Также заметим, что три пересекающиеся окружности S1, S2, S3 – задают инверсию. Образ произвольной точки К при этой инверсии задается проведением окружностей через К и пары точек пересечения этих трех окружностей.

Уточнение и мнимая инверсия.

Мы видели, что четыре точки А, В, С D, лежащие на одной окружности – определяют инверсию. Для этого достаточно разбить эти точки на две пары сопряженных между собой точек. Но разбить 4 точки на пары можно тремя способами.


Мы разобрали первый случай, когда сопряжены А и В, С и D. В этом случае – центр инверсии О1, он не разделяет А и В или С и D. Если сопряжены А и С, В и D то центр инверсии – О2, О2 опять-таки не разделяет эти пары точек. Но, при любом положении 4 точек на одной окружности их можно разбить на пары одним способом (и только одним) так, что точка пересечения прямых, проведенных через эти пары лежит внутри окружности, на которой эти точки лежат и, к тому же, эта точка пересечения, О3 – разделяет сопряженные точки. О3 разделяет А и D; С и В. В этом случае |O3, A|*|O3, D|=|O3, C|*|O3, B| по свойству хорд, но в отличие от обычной инверсии – А и D лежат по разные стороны от О. Как было сказано в ст. 1 – в этом случае мы имеем дело с мнимой инверсией, с центром в О3. «Мнимой» ее называют не потому, что она нам «кажется», а потому, что раз вектора О3А и О3D направлены в разные стороны, то произведение |O3, A|*|O3, D| – естественно считать отрицательным и оно равно квадрату мнимого числа. Это мнимое число называют радиусом мнимой инверсии. (Или радиусом мнимой инверсии называют равное ему по величине действительное число).
Вернемся к рисунку 8. Обозначим три инверсии с центрами в О1, О2, О3 (и меняющие местами точки внутри пар) соответственно I1, I2, I3. Можно показать, что для любой точки К I1(I2(K)=I2(I1(K)), I2(I3(K)=I3(I2(K)), I1(I3(K)=I3(I1(K)).
Это называется, что все эти инверсии коммутируют между собой. И также I1(I2(I3(K))) – снова инверсия, причем относительно окружности, на которой лежат точки А, В, С, D. Это будет доказано (вместе с рядом теорем про окружности на эту тему) в следующей статье. Сейчас же мы вернемся к понятию пучка окружностей.

Пучки окружностей


Мы уже несколько раз сталкивались с понятием «пучок окружностей». Это обобщение семейства окружностей, пересекающихся в одних и тех же двух точках. Проще всего его пространственное определение. Пусть в пространстве дана прямая А и сфера S. Окружности, которые высекают на сфере S всевозможные плоскости, проходящие через А – называются «пучком». Мы видели, что если А пересекается со сферой, то все эти окружности пересекаются в двух точках.


Такой пучок называют «действительным пучком». Точки пересечения окружностей называют «центрами пучка».
Если А касается сферы то получается


Этот случай называется «пучком касающихся окружностей». Точка касания называется центром пучка.
Если же прямая не имеет общих точек со сферой, то получается


Такой пучок называется «мнимым».
Пространственное определение удобно объединяет все эти случаи. Но оно не очень удобно для доказательства теорем. Поэтому я сейчас дам и другое определение пучков окружностей. Первые два случая (рисунки 9. и 10.) легко определить просто как семейство окружностей, имеющих одинаковые общие точки с двумя данными. В третьем случае (рисунок 11.) окружности не имеют общих точек. Но есть пара точек Р и Q, такие, что любая окружность I, лежащая в пучке – меняет их местами при инверсии (иначе говоря, эти точки инверсно сопряжены относительно любой окружности пучка) I(P)=Q. Как найти эти точки? (Если известны какие-то две непересекающиеся окружности А и В мнимого пучка).
Инвертируем В в А, полученное в В, затем снова в А, затем в В и так далее. Мы получим наборы стягивающихся к точкам окружностей (как бы отражения в двух зеркалах).
А, А(В), А(В(А)…стягивается к точке внутри А.
В, В(А), В(А(В)… стягивается к точке внутри В.
Эти точки стягивания и будут точками P и Q. Точки Р и Q называются центрами мнимого пучка.


Как расположены центры окружностей этого пучка?
Инверсия меняет местами Р и Q поэтому ее центр лежит на прямой (P, Q), чем дальше центр от Р и Q тем больше радиус окружности.
Если же центр лежит между Р и Q то есть мнимая инверсия, меняющая местами Р и Q. Радиус инверсии равен корню квадратному из произведения |O,P|*|OQ|. Заметим, что из любой точки плоскости можно провести одну и только одну окружность, лежащую в данном пучке. (если эта точка не совпадает с P или Q). Это можно показать, просто указав радиус и центр такой окружности с помощью элементарных вычислений. А можно по-другому, используя «непрерывность» изменения окружностей пучка. Мы можем считать, что окружности пучка изображают процесс возникновения окружности в точке Р, ее постепенного увеличения и затем стягивания к точке Q. Видоизменяясь так, окружность проходит через все точки плоскости. Заметим, что это свойство (из любой точки плоскости, не совпадающей с центром пучка, можно провести одну и только одну окружность данного пучка) – верно для пучков всех трех типов.
Также для пучков всех трех типов верно, что композиция инверсий относительно трех окружностей пучка – есть снова инверсия относительно какой-то окружности пучка. Т.е. если А, В, С – окружности одного пучка, то существует такая окружность D в этом пучке, что А(В(С(Х)))=D(Х) для любой точки Х. Это свойство можно взять за определение пучка окружностей, подробней мы его разберем далее (здесь и в следующих статьях).
Отметим еще, что пучок окружностей можно определить как совокупность окружностей, ортогональных двум данным.
1. Если данные окружности А и В не имеют общих точек, то совокупность ортогональных им окружностей образует действительный пучок.


О1, О2, О3 все проходят через точки Р и Q такие, что А(P)=Q и В(Р)=Q (т.е. P и Q являются центрами мнимого пучка, заданного окружностями А и В). Мы видим, что каждая окружности мнимого пучка ортогональна каждой окружности действительного пучка и наоборот. Такие пучки называются «сопряженными». Они создают своеобразную сетку координат. (Указанные свойства нетрудно доказываются, чтобы не уводить внимание в сторону это будет сделано не здесь, а в следующих статьях).
2. Если две исходные окружности А и В касаются в точке Р, также касаются друг друга в точке Р, касаются они и прямой, ортогональной общей касательной А и В.


Опять-таки пучок, в котором лежат А и В и пучок ортогональных им окружностей называют «сопряженными пучками». совместно они задают сетку координат, напоминающую, как и в прошлом случае, изображение силовых линий какого-то физического поля.
3. Если же окружности А и В пересекаются в точках P и Q, то ортогональные им окружности – это мнимый пучок с центрами в P и Q.


Этот случай был рассмотрен в п. 1

Теперь повторим еще раз обобщенную формулировку теоремы о шести окружностях:
Если есть три окружности А, В, С и окружность D лежит в одном пучке с А и В, а окружность Е в одном пучке с В и С то существует окружность F лежащая одновременно и в одном пучке с Е и D и в одном пучке с А и С. Если все указанные пучки действительны (т.е. мы имеем дело семействами пересекающихся окружностей), то утверждение означает то, что точки пересечения окружностей Е и Д и точки пересечения А и С – лежат на одной окружности. Именно с этой формулировки мы и начали изучать теорему о шести окружностях.
Мы можем сформулировать ее и иначе, используя часто встречавшееся уже разбиение на пары. Только сейчас мы разбиваем на пары не точки, а четыре окружности А, В, С, D.
Если при одном разбиении на пары, напр. (А, В) и (С, D) пучки окружностей, заданные этими парами соединимы, то и при любом другом разбиении на пары – будут соединимы образуемые этими парами пучки окружностей. То есть пучок (А, С) соединим с пучком (B, D), а пучок (А, D) с пучком (В, С).

Дополнение о прямых и точках на плоскости.


Как пример пучков, рассмотрим пучки на обычной евклидовой плоскости. Пучком прямых здесь называется совокупность прямых, проходящих через фиксированную точку плоскости или совокупность параллельных прямых.


Рассмотрим пучок прямых, проходящих через точку Р. Нетрудно показать, что последовательное выполнение двух симметрий относительно А2 и А1 (это обозначается А1*А2) есть поворот на удвоенный угол между ними. Если угол между А1 и А2 соразмерим с pi то последовательное выполнение этого поворота в конце-концов приведет любую точку Х обратно а ее образы при этих поворотах образуют вершины правильно многоугольника. Если же это угол не соразмерим с pi, то под действием поворота Х будет двигаться по окружности с центром в Р, постепенно заполняя ее всюду плотно.
Покажем, что А1*А2*А3 – (композиция трех симметрий относительно пересекающихся в одной точке прямых) – симметрия относительно прямой, проходящей через их точку пересечения. А1*А2 – это поворот на удвоенный угол между прямыми, центр поворота Р. Поэтому А1*А2 дает тот же поворот, что и композиция В*А3 если угол между В и А3 равен углу меду А1 и А2 и угол отложен в том же направлении.
А1*А2=В*А3 следовательно (А1*А2)*А3=(В*А3)*А3=В*(А3*А3)=В (мы можем раскрывать скобки, когда считаем композиции симметрий или произвольных преобразований, и одна симметрия, дважды примененная – ничего не изменяет). Итак А1*А2*А3=В, что и требовалось.


Рассмотрим теперь пучок параллельных прямых.


А1*А2 – это параллельный перенос на удвоенное расстояние между прямыми А2 и А1 в направлении перпендикулярном этим прямым. Совершенно аналогично предыдущему случаю вводим прямую В так, чтобы А1*А2=В*А3 (отложив В на том же расстоянии от А3, что между А2 и А1 и в той же стороне). Точно также как в предыдущем случае А1*А2*А3=В.
Заметим, что между пересекающимися прямыми есть угол, а между параллельными – угла нет (или он равен нулю всегда), но можно измерить расстояние.
Интересно, что композиция трех точечных симметрий – всегда снова точечная симметрия. Это тривиально доказывается:
1. Композиция двух точечных симметрий относительно точек А и В есть параллельный перенос на удвоенный вектор с началом в оной точке и концом в другой.


Вектор с началом в Х и концом В(А(Х)) есть удвоенный вектор с началом в А и концом в В. Что и требовалось. еще заметим, что точечная симметрия есть композиция симметрий относительно перпендикулярных прямых, пересекающихся в этой точке.


А как выглядела бы наша теорема о пучках, если попытаться перенести ее на прямые?
Даны четыре прямые А, В, С, D. Пучки (А, В) и (С, D) – соединимы. Следовательно и пучок (В, С) и пучок (А, D) – соединимы и пучки (А, С) с (В, D) – соединимы. Это – верно, но бессодержательно, т.к. на плоскости соединимы все пучки прямых (за одним исключением), т.к. всегда есть прямая, проходящая через центры пучков (точки пересечения прямых пучка). Или, если одни из пучков – параллельные прямые – существует прямая, параллельная им и проходящая через центр второго пучка. Единственный пример несоединимых пучков в данном случае – это два пучка параллельных прямых.


Пучки несоединимы, т.к. нет прямой параллельно одновременно А1 и В1.

Связь пучков окружностей и пучков прямых.


В завершение укажем на связь между пучками прямых и пучками окружностей. Покажем, что пучки прямых эквивалентны (изоморфны) пучкам окружностей, имеющих общую точку.
Действительный пучок окружностей.


Осуществим инверсию с центром в Q (одной из точек пересечения окружностей пучка). Все окружности пучка перейдут в прямые, точка Q – в бесконечно удаленную точку. Получится пучок прямых, пересекающихся в точке Р (см. рис. 17.) Инверсии относительно окружностей пучка – теперь привычные нам симметрии относительно прямых.
Пучок касающихся окружностей.


Осуществим инверсию с центром в точке касания окружностей, окружности перейдут в параллельные прямые.
Поэтому, доказав, что А*В*С есть снова симметрия относительно прямой, где А, В, С – прямые, проходящие через одну точку или параллельные друг другу, мы доказали и то, что если А, В, С – окружности из одного пучка (действительного или касательного), то А*В*С – инверсия относительно окружности из этого пучка. (Подобней это будет разъяснено в следующих статьях). Случай, когда А, В, С из одного мнимого пучка – остался недоказанным.
Используются технологии uCoz