Статья 4.

Моделирование проективной геометрии с помощью геометрии окружности и сферы.

Краткое содержание статьи.

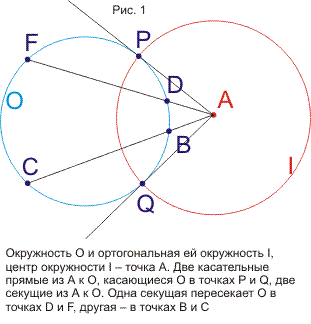
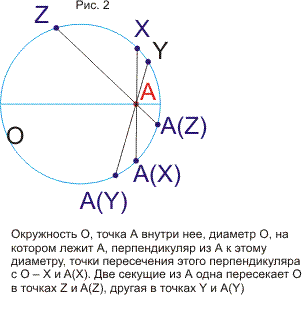
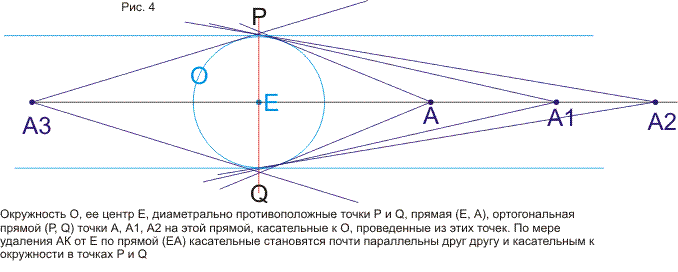
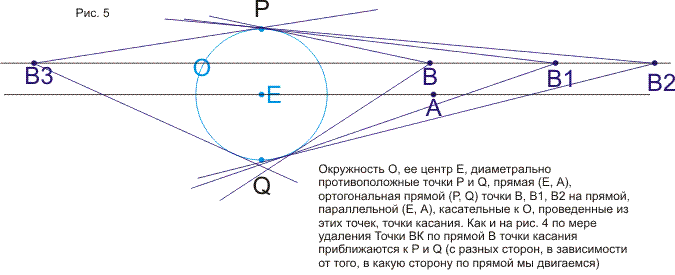
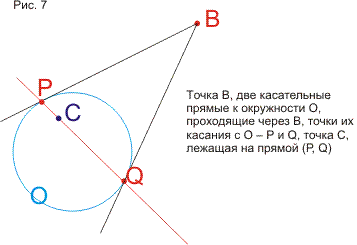
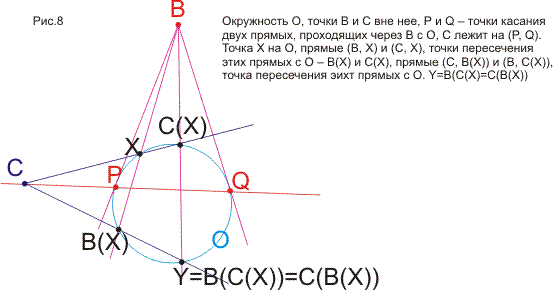
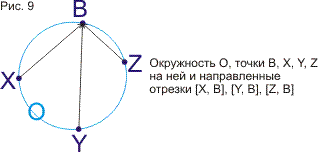
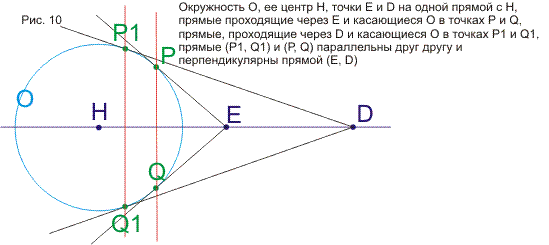
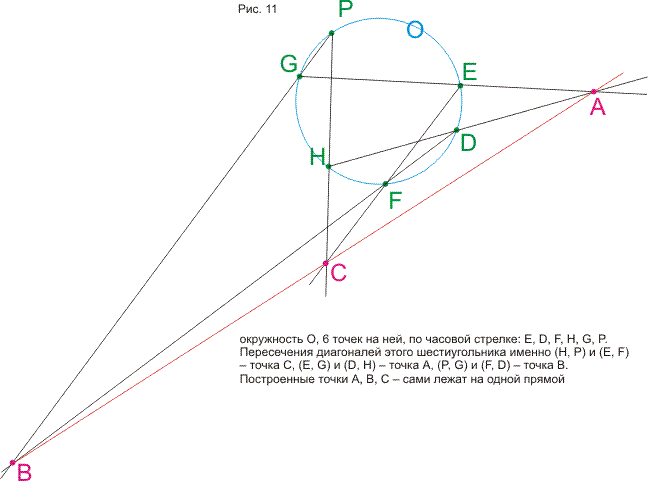
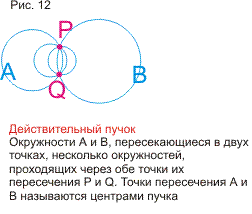
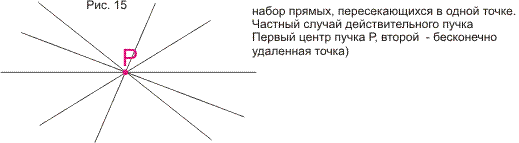
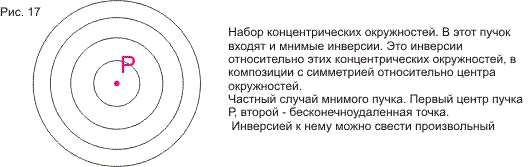
В статье строится наглядная модель проективной плоскости и проективного пространства на основе геометрии окружности. Дается наглядное геометрическое истолкование алгебраических соотношений (А*В*С)2=е и А*В=В*А (коммутативность). Показывается связь этой модели с исчислением бесконечно-малых и связь тождества (А*В*С)2=е с теоремой Паскаля. В приложении кратко формулируются основные свойства пучков и разъясняется рассмотрение точки как частного случая окружности. Статья подготавливает к моделированию и изучению геометрий Римана, Евклида и Лобачевского методами геометрии окружности. В несколько другом ракурсе тема рассмотрена в моей статье, опубликованной в журнале «Математическое просвещение» (№3, 1999 год)

Моделирование проективной плоскости.
А-отображения.

Уже когда в ст. 2 мы доказывали теорему о пучках, то воспользовались тем, что окружность на сфере – лежит в некоторой плоскости и свойства пересечений окружностей на сфере можно соотнести со свойствами пересечений прямых и плоскостей в пространстве. То есть – с проективным пространством. В этой статье мы систематически покажем связь между проективной геометрией: геометрией прямых, точек и плоскостей с геометрией окружности. Начнем с плоского случая.
Рассмотрим произвольную окружность О и совокупность ортогональных к ней окружностей. Каждой точке плоскости (кроме лежащей на самой окружности О) соответствует одна и только одна инверсия, ортогональная О.


В самом деле, пусть А произвольная точка вне О – центр некоторой окружности I, ортогональной О. Тогда в А, по определению инверсии, пересекаются все прямые, проходящие через образ и прообраз точки (под действием этой инверсии). По теореме о секущих из точки А (мы пользовались ею, напр., доказывая теорему о пучках)
|A, A(B)|*|A, B|=|A, D|*|A, A(D)|=|A, A(P)|*|A, P|=|A, P|2
Здесь через А(В) обознается образ точки В при инверсии относительно окружности I (с центром в А и ортогональной к О). Р – точка касания прямой проходящей через А с О, поэтому А(Р)=Р, радиус инверсии равен |A, P|. Эта инверсия действует на в сю плоскость, но нам ближайшем будущем будет важно только ее действие на окружность О. Также на ближайшее время мы можем забыть про окружность I. Нам будет важна лишь точка А – центр инверсии. Ведь точка А полностью задает отображение окружности О в себя. Чтобы найти образ произвольной точки Х, лежащей на О при этом отображении надо:
1. Провести прямую (А, Х).
2. Найти вторую точку пересечения (А, Х) и О (первая точка пересечения – Х).
3. Эта точка и будет образом точки Х при отображении, заданном точкой А.
Назовем это отображение – «А-отображением окружности в себя». Точку, определяющую отображение назовем «центром отображения». Если (А, Х) касается О, то мы определяем, что А(Х)=Х, Х – неподвижная точка при А-отображении. А-отображение окружности О в себя можно продолжить на всю плоскость и это будет инверсия относительно окружности I. Но, как было сказано, пока мы интересуемся как действует А-отображение на окружность О.
Заметим еще, что если Р и Q неподвижные точки А-отображения, то любая пара точек Х и А(Х) гармонически разделяет пару Р и Q. (Понятие гармонического отношения играет важнейшую роль в проективной геометрии, но в этой статье я не буду его исследовать).
Если точка А лежит внутри окружности О, то точки пересечения любой прямой, проходящей через А с окружностью О лежат по разные стороны от А. Поэтому А определяет мнимую инверсию.


По теореме о хордах: |A, Z|*|A, A(Z)|=|A, Y|*|A, A(Y)|=A, X|*|A*, A(X)|. Это задает мнимую инверсию с центром в А. Как и должно быть при мнимой инверсии – неподвижных точек нет, т.к. если А лежит внутри О, то невозможно провести из А прямую, касающуюся О. Радиус инверсии R равен корню квадратному из указанного произведения. Геометрически его можно найти из того, что R=|A, X|, если |A, X|=|A, A(X)|. А это равенство достигается, если отрезок [X, A(X)] – перпендикулярен диаметру О проходящему через А, как это и изображено на рис. 2. пять-таки, мы будем рассматривать действие этой мнимой инверсии только на окружность О, а действие ее на остальные точки плоскости нам пока будет не интересно.
Итак, мы видим, что всякая точка плоскости, не лежащая на окружности О задает одну и только одну инверсию плоскости, при которой окружность О переходит в себя. Если А вне окружности – это обычная действительная инверсия, если внутри – мнимая. При изучении действия этих инверсий на О можно пользоваться описанными выше А-отображениями (образ точки Х на окружности О есть вторая точка пересечения прямой (А, Х) с О). Тривиально доказывается, что А(А(Х))=Х (иначе говоря, А(Х) – инволютивное отображение).
Пусть А – вне окружности. (Рис. 1). В этом случае у А-отображения есть две неподвижные точки Р и Q. Заметим, что А-отображение как бы выворачивает наизнанку окружность О, меняя местами две дуги, на которые разделили окружность точки Р и Q. Это напоминает, как инверсия на плоскости меняет местами внутренность и внешность неподвижной окружности инверсии. Мы можем еще сказать, что пара точек Р и Q окружности О задает инволютивное отображение (или симметрию) окружности О в себя. Нужно провести касательные к О и найти их точку пересечения между собой. Эта точка и задаст требуемое А-отображение окружности. Заметим, что для определения этого отображения нам пришлось «выйти за пределы» окружности О.
Указанный прием не работает в одном случае. Если точки Р и Q – диаметрально противоположные точки на окружности О. Тогда касательные в этих точках будут параллельны друг другу и не пересекутся на евклидовой плоскости.


Чтобы догадаться, какое отображение О в себя задают точки Р и Q можно вспомнить, что мы говорили про ортогональные к О окружности. Окружность, ортогональная к О и проходящая через пару диаметрально противоположных точек на О – прямая. (Как было сказано, прямая, это окружность с бесконечно удаленным центром.) проведем эту прямую I. Симметрия относительно этой прямой переводит окружность О в себя, оставляя точки Р и Q неподвижными. Мы видим, что каждая пара точек на окружности О задает «инверсию» или симметрию этой окружности. Заметим сходство с объемным случаем. Окружность на сфере задает инверсию сферы, при этом окружность лежит на некоей плоскости, секущей сферу; пара точек на окружности задает инверсию окружности, причем пара точек, разумеется, лежит на некоей прямой, секущей сферу.
Симметрию относительно прямой, проходящей через центр окружности О как частный случай А-отображений можно получить с помощью ПРЕДЕЛЬНОГО ПЕРЕХОДА.


Пусть точка А удаляется от окружности О по прямой (А, Е), проходя через точки А1, А2… Мы видим, что касательные к О, проходящие через точки А, А1, А2 – касаются О в точках, все ближе расположенных к P и Q, где Р и Q – концы диаметра, перпендикулярного к (А, Е). А отображения: А(Х), А1(Х), А2(Х) все более напоминают симметрию относительно прямой (Р, Q). Секущие же из точек А, А1, А2 – все более приближаются к параллельным к прямой (А, Е).
Пусть теперь какая-нибудь точка В двигается по прямой, параллельной (А, Е) в ту же сторону, что и А.


Мы видим, что неподвижные точки отображений В(Х), В1(Х), В2(Х) – приближаются к точкам P и Q, а сами отображения все более напоминают симметрию относительно прямой (Р, Q), а секущие, проходящие через В, В1, В2 все ближе к параллельным к (А, Е) прямым (угол между секущими уменьшается). Это аналогично тому, как изменяется угол падающих лучей при удалении источника света. Заметим еще, что если точка С расположена на прямой (А, Е) по другую сторону от О чем точка А и удаляется все далее от О, то с удалением С С(Х) опять-таки приближается к симметрии относительно прямой (Р, Q).
Симметрии окружности О относительно прямых, проходящих через ее центр – мы также будем называть А-отображениями, имея в виду, что их центр – бесконечно удален от А, совпадая с точкой пересечения касательных к О в диаметрально противоположных точках. Каждому «направлению удаления от О» отвечает перпендикулярная ему прямая, проходящая через центр окружности О.

Алгебраические свойства А-отображений,
их геометрическое истолкование.

Зададимся теперь вопросом, когда А-отображения коммутируют (т.е. безразличен порядок, в котором их применять к окружности О). Пусть В(Х) и С(Х) два А-отображения и они коммутируют, то есть С(В(Х))=В(С(Х)) для всех Х. В том числе это равенство должно выполняться и для тех Х, при которых В(Х)=Х, т.е. на неподвижных точках отображения В. Подставим С(В(Х))=С(Х) т.к. В(Х)=Х. С(В(Х))=В(С(Х))=С(Х) т.е. из коммутируемости В(Х) и С(Х) следует, что, что если Х – неподвижная точка отображения В, то С(Х) – также неподвижная точка отображения В, иначе говоря, С как-то переставляет неподвижные точки отображения В. аналогично, В как-то отображается неподвижные точки отображения С в себя.
Мы знаем, что у всякого А-отображения 2, 1 или ни одной неподвижной точки в зависимости от того, лежит центр А-отображения вне, на или внутри окружности О. Разберем случай, когда неподвижных точек 2. Пусть это точки Р и Q. В(Р)=Р, В(Q)=Q. С отображает эту пару точек в себя. Возможны два случая:
1. С(Р)=Q, C(Q)=P
2. C(P)=P, C(Q)=Q (C как и В, оставляет точки P и Q неподвижными.)
Что означают эти случаи геометрически? Первый случай означает, что С – лежит на прямой, проходящей через Р и Q.


Второй случай означает, что С лежит на прямой, касающейся О в точке Р и на прямой, касающейся О в точке Q, т.е. в точке пересечения этих прямых. Но это – точка В. Если точка С совпадает с точкой В, разумеется, эти отображения коммутируют. Они просто совпадают друг с другом, а всякое отображение коммутирует само с собой. Но это случай мы не будем рассматривать.
Итак, нам интересен только случай 1., когда С – меняет местами неподвижные точки отображения В (точки Р и Q). Мы покажем, что условие «С лежит на прямой, проходящей через точки Р и Q – не только необходимо, но и достаточно. Точнее – я сошлюсь на давно известные геометрические факты, из которых это следует.


На рисунке по данным точкам Х, С, В, построены точки В(Х), С(Х), С(В(Х)), В(С(Х)). Коммутируемость отображений С и В означает, что точки С(В(Х)) и В(С(Х)) совпадают, т.е. прямые (С, В(Х)) и (В, С(Х)) – пересекаются в одной точке (при том условии, что С лежит на прямой (Р, Q)). Можно сформулировать и иначе: при данном условии (что С лежит на (Р, Q)) если пара точек окружности О лежит на одной прямой с В, то прямые, проведенные через С и эту пару точек – пересекают О в точках, также лежащих на одной прямой с В.
Есть геометрическая теорема доказывающая этот факт. Мы не будем здесь приводить это доказательство. Но некоторые определения, связанные с теоремой нам понадобятся. Теорема обычно доказывается в рамках теории «поляр и полюсов». Дадим ключевое определение этой теории:
Пусть дана точка В вне (или на) окружности О и проведены касательные прямые к окружности О через эту точку. Прямая L, проходящая через точки касания этих прямых с О – называется полярой точки В. А точка В называется полюсом прямой L. В терминах А-отображений это звучит так: «полярой точки В называется совокупность таких точек, что А-отображения с центрами в этих точках – меняют местами неподвижные точки отображения В».
Первое свойство поляр – взаимность. Если какая-то точка Х лежит на поляре точки В, то и В лежит на поляре Х. Второе свойство – двойственность: если три точки лежат на одной прямой, то их поляры пересекаются в одной точке. Предлагаю читателю самостоятельно сформулировать это свойство в терминах А-отображений.
Из приведенной выше геометрической теоремы следует, что если точка С лежит на поляре В, то А-отображения с центрами в этих точках – коммутируют. И, обратно – если А-отображения коммутируют, то они лежат на поляре друг друга. Обратим внимание на связь свойства взаимности поляр с коммутируемостью. Если В коммутирует с С, то и С коммутирует с В – именно этот очевидный факт и выражает свойство взаимности.
Мы рассматривали случай, когда В лежит вне окружности О. Если В лежит на О, то полярой В называют касательную прямую к О в точке В. А если В лежит внутри О?
В этом случае полярой В называют совокупность точек, которые являются полюсами прямых, проходящими через В. По свойству двойственности – эти точки лежат на какой-то одной прямой. Эта прямая и будет полярой точки В. Заметим, что в данном случае поляра не имеет общих точек с О. Ведь полюс прямых, пересекающих О – вне О. В терминах А-отображений можно сказать, что полярой точки В называют совокупность точек С, таких, что А-Отображения с центрами в точках В и С коммутируют между собой. Заметим, что приведенное определение охватывает случаи, когда В вне или внутри О. Более того, если В лежит на О, мы также можем связать с ней отображение: В(Х)=В какой бы ни была Х.


В(Х)=В(Y)=B(Z)=В. Это отображение, конечно, не будет взаимнооднозначным, тем более – инволютивным. Образ всех точек одинаков – точка В. Но вопрос про коммутативность имеет смысл. Пусть А-отображение с центром в С коммутирует с описанным только что отображением В(Х)=В С(В(Х))=В(С(Х)) левая часть равна С(В) правая – В. Значит С(В)=В, а это равносильно тому, что С лежит на поляре В (прямой касающейся О в В). Заметим, что рисунок 9 прямо-таки подводит к мысли о связи этой темы с исчислением бесконечно малых (окружность отображается в бесконечно-малую окрестность точки В). Теперь мы можем сформулировать аксиомы о прямых и точках в терминах А-отображений. Это будет несколько хитроумно. Пусть Е и D – две точки плоскости. Они задают А-отображения с центрами в этих точках. Есть одно и только одно отображение, коммутирующее с ними обоими. Обозначим его В. Совокупность всех А-отображений, коммутирующих с В мы и назовем «прямой, проходящей через Е и D» Это определение вызывает вопросы. Почему есть одна и только одно А отображение, коммутирующей с E и D?
Все центры А-отображений, коммутирующих с Е лежат на поляре к Е, а все центры А-отображений, коммутирующих с D на поляре к D. Если эти две прямые пересекаются, то точка их пересечения и будет центром искомого отображения. Если эти две прямые параллельны (а это возможно только если Е и D лежат на одной прямой с центром окружности О, то искомым отображением будет осесимметрия относительно (Е, D)


Предоставляю читателю самостоятельно доказать, что в этом случае (если поляры Е и D параллельны – Е и D лежат на одной прямой с центром окружности О и симметрия относительно (Е, D) коммутриует с А-отображениями с центрами в Е и D.
Итак, мы доказали, что отображение В, коммутирующее с Е и D – только одно. Поэтому пара А-отображений с центрами в Е и D в самом деле однозначно задают совокупность А-отображений, таких, что они коммутируют с коммутирующим с Е(X) и В(Х) отображением. Теперь надо доказать, что определенные таким образом «прямые» – всегда пересекаются в одной точке, т.е. что есть одно и только одно А-отображение, лежащее в обоих множествах точек. Но, по сути, мы это уже сделали. Допустим А-отображения первой прямой все коммутируют с В1 (иначе говоря В1 является полюсом этой прямой), а второй прямой – с В2 (В2 является полюсом этой прямой). Есть одно только одно А-отображение, коммутирующее с В1 и В2 одновременно, оно и будет искомым пересечением двух определенных таким образом прямых. Заметим, что в некоторых случаях точки пересечения могут лежать на окружности О. Точка лежащая на О, как было показано, также задает отображение, которое мы и рассматриваем в данном случае.
Повторим: А-отображения называются лежащими на одной прямой, если существует какое-то А-отображение, коммутирующее с каждым из них. Замечательно, что центры этих А-отображений изображаются точками, лежащими на одной прямой! См. Рисунок 8.
Итак, мы показали, что А-отображения моделируют проективную плоскость.

Теорема Паскаля и А-отображения,
уравнение (S*T*F)2=e.


Теперь мы установим связи между А-отображениями и теоремой Паскаля. Для этого вспомним, что А-отображения это – действия инверсий на ортогональную им окружность О. А отображения, лежащие на определенной нами прямой по определению – коммутируют с неким А-отображением. Обозначим Его В. Значит и инверсии, сужением которых и являются А-отображения) коммутируют с В. кроме того, эти инверсии коммутируют с О. Но тогда они лежат в одном пучке (двойственном к пучку, в котором лежат А и О см. ст. 2). А все инверсии из одного пучка имеют свойство: композиция любых трех из них – инволютивна, снова инверсия относительно окружности (действительной или мнимой) из этого пучка. То есть для любых трех инверсий S, T, F из одного пучка S(T(F(S(T(F(X))))))=Х или, выражаясь иначе (S*T*F)2=e. Теперь проиллюстрируем теорему Паскаля.


Теорема Паскаля утверждает, что если шесть точек Е, D, F, H, G, P – лежат на одной окружности, то точки пересечения диагоналей, указанных на рисунке – лежат на одной прямой. Рассмотрим А-отображения с центрами в точках пересечения этих диагоналей: С, А, В. Заметим, что А(Р)=G, A(D)=F, B(E)=G, B(D)=H, C(P)=H, C(E)=F. Начнем построение с точки Р. Выразим оставшиеся 5 точек с помощью композиций А-отображений. G=A(P), E=B(A(P)), F=C(E)=(C(B(A(P))), D=A(F)=A(C(B(A(P)))), H=B(D)=B(A(C(B(A(P))))), и P=C(H)=C(B(A(C(B(A(P)))))). Обозначим отображение C*B*A буквой К. Мы только что показали, что К(К(Р))=Р или, что К инволютивна на точке Р, т.е. С*В*А инволютивно на точке Р. Рассказанного в предыдущих статьях недостаточно, чтобы заключить отсюда, что К= C*B*A инволютивна на всех точках. (а этого было бы достаточно для доказательства теоремы Паскаля). Но мы можем сформулировать родственное ей утверждение:
Из того, что А, В, С – лежат на одной прямой, следует, что построение замкнется или, что точки С, Р, Н – лежат на одной прямой. Это следует из того, что если А, В, С лежат на одной прямой, то С*В*А – инволютивно и образы точки Р связаны описанными выше соотношениями.
Заметим, что свойство (А*В*С)2=е можно было бы взять за определение «прямой» то есть определить так: три точки А, В, С лежат на одной прямой только если композиция А-отображений с центрами в них – снова есть какое-то А-отображение. Но тогда бы мы столкнулись с одной трудностью: точки лежащие на О не подпадали бы под это определение. Если одна из этих точек лежит на О, то она отобразит все точки О в себя и, разумеется, композиция с участием такой точки не будет инволютивна. Чтобы обойти эту трудность, вероятно надо развить идею, что точка на О – это не точка, а бесконечно малая окрестность. Но это отдельная тема.

Моделирование проективного пространства.


Можно очень просто сформулировать соответствие между плоской геометрией окружности и геометрией проективного пространства.
А. Назовем «точкой» проективного пространство инверсию (действительную или мнимую) или точку геометрии окружности
В. Назовем «прямой» проективного пространства – совокупность инверсий, ортогональных двум данным и, если эти инверсии действительные – то и их общие точки (если эти точки есть).
С. Назовем «плоскостью» проективного пространства – совокупность инверсий и, если данная инверсия действительная – совокупность лежащих на ней точек.
Пояснения.
1. Я говорю «ортогональные», а не «коммутирующие». Разумеется, это вольность речи. Инверсии это – отображения, а не геометрические объекты.
2. Я трактую здесь точки как частный случай инверсий. Поскольку определения используют лишь одной свойство инверсий – коммутируемость (ортогональность) это корректно. Ведь точку можно считать ортогональной к окружности, на которой она лежит. Фактически я мыслю здесь точки как «очень маленькие окружности». Такой ход мысли хотя и непривычен, все же имеет больше общего с реальностью, чем представление о точке, как о чем-то лишенном толщины, и т.п. как это принято обычно.
Аналогично тому, как через три точки всегда можно провести окружность – для трех инверсий всегда есть инверсия, ортогональная им всем. Если инверсия мнимая – она не ортогональна ни одной точке.
Прямая проективной геометрии – это просто пучок окружностей (инверсий). Раз мы считаем точки частным случае окружностей, то пара точек также должна задавать пучок. Это будет – мнимый пучок с центрами в этих точках. Точка и окружность также задают мнимый пучок, его центры: исходная точка и образ этой точки относительно данной окружности.
Дав эти определения нам нужно многое доказать, чтобы убедиться, что определенные так «точки, прямые и плоскости» ведут себя так, как мы привыкли или, как это должно быть в проективной геометрии.
1. Что пара точек «точек» задает «прямую». Это равносильно тому, что две произвольные инверсии (или точки) задают совокупность инверсий и точек, ортогональных неким двум инверсиям (или точкам) и сами эти исходные инверсии ортогональны этим «неким».
2. Что для любых трех инверсий существует инверсия, ортогональная им. Это означает, что через любые три точки проективного пространства можно провести плоскость.
И еще ряд аналогичных утверждений нам надо доказать. Мы сделаем это во второй части статьи. Пока же мы построим наглядную пространственную модель, которая объяснит нам, в чем суть дела. Я сделаю эту модель с помощью А-отображений в пространстве. Определяются А-отображения в пространстве точно также, как А-отображения на плоскости.
Пусть S – сфера в пространстве, F – произвольная точка не лежащая на сфере, Х – произвольная точка на сфере S. проведем через X и F прямую, она пересечет S в некоей точке Y. Y и будет образом точки Х при А-отображении с центром в точке F, (а Х будет образом точки Y при этом отображении, F(F(X))=X для всех Х, т.е. F(X) – инволютивное отображение). Возможно, что прямая (Х, А) касается сферы S. В этом случае определяем F(X)=X. Разберем свойства неподвижных точек при таких отображениях. Если F лежит внутри сферы S, то всякая прямая, проходящая через F – пересекает сферу в двух различных точках, поэтому у А-отображения с центром в F нет неподвижных точек. Если F снаружи сферы S, то неподвижные точки А-отображения с центром в F лежат на прямых, проходящих через F и касающихся S. Точки касания этих прямых и будут неподвижными точками А-отображения с центром в F. Прямые, проходящие через F и касающиеся S образуют конус (с вершиной в F), а линия касания этого конуса со сферой – окружность. (Это следует из того, что описанное построение можно повернуть на любой угол, относительно прямой, проходящей через F и центр сферы). Таким образом, мы имеем сейчас колпак, надетый на сферу.
Итак, если F – вне сферы, то неподвижные точки А-отображения с центром в F – окружность. Из определения видно, что А-отображение с центром в F в данном случае «выворачивает» сферу S относительно неподвижной окружности. Есть несколько способов показать, что А-отображения отображают окружности на сфере – в окружности и являются инверсиями (действительными, если F лежит снаружи сферы и мнимыми, если внутри). Я укажу два. Первый: точно также, как А-отображения на плоскости можно расширить до инверсий, ортогональных окружности О, так и А-отображения в пространстве можно расширить до инверсии сфер, ортогональных сфере S. второй: воспользоваться теорией поляр и полюсов в пространстве.
Полярой точки F лежащей снаружи сферы называют плоскость, в которой лежит окружность, неподвижная при А-отображении с центром в F. (Окружность касания конуса с вершиной F и сферы S). Точно также, как в плоском случае есть свойство взаимности: если точка а лежит на поляре точки В, то и точка В лежит на поляре точки А. Если четыре точки лежат на одной плоскости, то четыре их поляры – пересекаются в одной точке. Есть важная особенность теории поляр в пространстве: каждой прямой можно сопоставить прямую. Именно, пусть прямая L есть пересечение двух плоскостей А и В. Рассмотрим полюса этих плоскостей и проведем через эти две точки прямую М. Она и будет соответственной к L прямой. (или возьмем две точки на L, проведем поляры этих точек, они пересекутся по некоторой прямой, которая совпадет с построенной другим способом М).
Можно конечно доказывать свойства А-отображений не используя ни теорию инверсий в пространстве, ни теорию поляр и полюсов, а сводя дело к серии задач по стереометрии. Заметим еще, что А-отображения из-за их наглядности можно использовать для определения инверсий на сфере. Если центр А-отображения F лежит снаружи сферы, то F задает действительную инверсию, относительно окружности неподвижных точек А-отображения с центром в F, если F внутри сферы, то F задает мнимую инверсию, у которой нет неподвижных точек.
Как и в плоском случае зададимся вопросом: когда А-отображения коммутируют. И ход рассуждений и результат будут напоминать рассуждения про А-отображения на плоскости. Пусть В и С – два коммутирующих А-отображения. В(С(Х))=С(В(Х)). Пусть у отображения с центром в точке В – есть неподвижные точки, т.е. В – вне сферы S. Тогда С отображает неподвижные точки отображения В – снова в неподвижные точки отображения В. Т.к. неподвижные точки этого отображения – окружность, то центры А-отображений, отображающие эту окружность в себя обязательно лежат в той же плоскости, что и эта окружность. Эта плоскость является полярой точки В. Мы показали, что В обязательно должно лежать на ней. В теории поляр доказывается, что этого достаточно, что если С лежит на поляре В, то А отображения с центрами в этих точках коммутируют друг с другом. Геометрически коммутирование отображений с центрами в А и В означает, что для любой точки Х на сфере S пара точек Х, В(Х) под действием отображения С переходит в пару точек, лежащую на одной прямой с В. (ср. рис. 8).
Резюмируем. Если В вне S, то центры коммутирующих с В отображений лежат на поляре В. Эта поляра пересекает сферу S. Те точки, которые лежат внутри S являются центрами А-отображений, определяющих мнимые инверсии, коммутирующие с В, а точки, лежащие снаружи определяют действительные инверсии, коммутирующие с В. Если же В внутри S, то центры коммутирующих с В А-отображений также лежат на поляре В. Эта поляра не имеет с S общих точек, все точки этой поляры лежат вне S и определяют действительные инверсии, коммутирующие с В. Заметим, что поскольку в данном случае В задает мнимую инверсию, то и коммутирую с ней только действительные инверсии. Это соответствует тому, что не существует двух коммутирующих друг с другом мнимых инверсий. Наконец, если В лежит на S, то мы можем определить отображение, отображающее все точки сферы в точку В. С этим отображением коммутируют все А-отображения, центры которых лежат на плоскости, касающейся сферы S в точке В. Эта плоскость называется полярой точки В. Все точки, кроме самой точки В задают действительную инверсию, коммутирующую с отображением всей сферы в точку В.
Итак, мы показали, что центры А-отображений, коммутирующих с данным – лежат на одной плоскости в трехмерном пространстве. «Прямая» по нашему определению – совокупность А-отображений (или инверсий на сфере) коммутирующих с двумя данными. Центры А-отображений, ортогональных двум данным лежат на пересечении плоскостей, где находятся центры А-отображений, ортогональных каждому из двух данных. Поэтому «прямая» в нашем определении – изображается пересечением двух плоскостей, т.е. – прямой в трехмерном пространстве. Случай, когда плоскости или прямые параллельны друг другу – разрешается аналогично плоскому варианту.
А тот факт трехмерной проективной геометрии, что любые три плоскости пересекаются в одной точке эквивалентентен в нашей модели тому, что для любых трех окружностей есть одна, ортогональная всем трем (это будет доказано в приложении).
В завершение этой темы восполним один пробел. Я несколько раз (уже в ст. 2) свободно переходил от изучения окружностей на плоскости к изучению окружностей на сфере, но не доказывал, что это можно делать (напр., доказывая теорему о пучках). Для доказательства правомерности этого перехода я приведу отображение сферы на плоскость, при котором точки сферы перейдут в точки на плоскости, окружности перейдут в окружности и углы между окружностями – также сохраняются. Иначе говоря – установлю изоморфизм (см. конец ст. 3) между геометрией окружностей на сфере и геометрией окружностей на плоскости. Это отображение называют стереометрической проекцией.
Пусть сфера S лежит на плоскости А и Р – наиболее удаленная от А точка сферы. (S касается А в точке под Р). Спроецируем сферу S на плоскость А при этом центр проекции поместим в Р. При этой проекции образом точки Х на сфере будет точка пересечения прямой (Р, Х) с плоскостью А. при этой проекции в каждую точку плоскости отображается одна точка сферы, но у точки Р, центра проекции нет образа. Тогда плоскость А пополняют «бесконечно удаленной точкой» (той самой, куда при инверсии переходят центр окружности) и говорят, что эта бесконечно удаленная точка и будет образом точки Р. Доказательство, что при этой проекции окружности переходят в окружности и углы между окружностями сохраняются – я здесь приводить не буду, ради экономии места. Его можно найти, например в книге Гильберта «Наглядная геометрия».

Приложение.
Основные свойства пучков окружностей.


Здесь будут кратко и по возможности полно перечислены основные свойства пучков и доказаны утверждения о пучках, важные для первой части этой статьи. Некоторые части статьи будут повторять уже изложенное в ст. 2.
Пучки можно определить, как семейство окружностей, «однородных» с двумя данными. Если две данные окружности А и В пересекаются, то это – семейство окружностей, проходящих через их точки пересечения. Такое семейство называется действительным пучком окружностей.


Точки пересечения А и В называются центрами пучка.
Если две окружности А и В касаются друг друга, то они задают пучок окружностей, касающихся их и друг друга. Этот пучок называют «касающимся» пучком.


Точку касания А и В называют центром пучка.
Если две окружности А и В не имеют общих точек, то они определяют мнимый пучок. Он определяется сложнее. Найдем пару точек Р и Q такую, что A(P)=Q, B(P)=Q. Всякая окружность Х, такая, что Х(Р)=Q лежит в пучке, определенном Р и Q, Иными словами, все окружности мнимого пучка одинаково действуют на какую-то пару точек Р и Q. В этот пучок входят и мнимые инверсии, меняющие точки Р и Q местами.



Ортогональность и пучки.


Также пучки окружностей можно определять используя свойство ортогональности. В основе определения лежит следующий факт: если окружность ортогональная каким-то двум окружностям из одного пучка, то она ортогональна всем окружностям из этого пучка. Благодаря этому произвольный пучок окружностей можно определить как совокупность окружностей, ортогональных двум данным А и В. Если А и В пересекаются, им ортогонален мнимый пучок. Если А и В касаются, им ортогонален касающийся пучок. Если А и В не имеют общих точек, им ортогонален действительный пучок.
Свойства пучков можно изучать, пользуясь инверсией в одном из центров изучаемого пучка. При этой инверсии этот центр пучка перейдет в бесконечно удаленную точку. Действительный пучок при инверсии перейдет в пучок прямых, проходящих через одну точку (эта точка будет образом второго центра пучка при этой инверсии).


Касающийся пучок перейдет в пучок параллельных прямых.


Мнимый пучок перейдет в семейство концентрических окружностей. Их общий центр – образ второго центра пучка при рассматриваемой инверсии.


В этот пучок входят и мнимые инверсии. Это инверсии относительно этих концентрических окружностей, в композиции с симметрией относительно центра окружностей.
Пользуясь приведенными рисунками легко доказать, что для любых трех инверсий А, В, С из одного пучка А*В*С – снова инверсия из этого пучка.
Если все окружности одного пучка ортогональны всем окружностям второго – эти пучки называются двойственными. Совместное изображение двойственный пучков напоминает своеобразную сетку координат или силовые линии.
Центры окружностей, лежащих в одном пучке, расположены на одной прямой (или совпадают, если эти окружности концентрические). В действительном пучке центры входящих в него окружностей лежат на прямой, равноудаленной от центров пучка (точек пересечения окружностей). В касающемся пучке центры окружностей лежат на прямой, ортогональной их общей касательной и проходящей через общую точку касания. В мнимом пучке центры окружностей лежат на прямой, проходящей через центры пучка. Причем точки, лежащие между центрами пучка – являются центрами мнимых инверсий этого пучка.
При моделировании проективной геометрии нам понадобилось рассматривать точки, как частный случай окружностей. Тогда мы считаем, что пара точек задает мнимый пучок с центрами в этих точках, точка Р и окружность А задают мнимый пучок с центрами Р и А(Р). Если Р лежит на А, то они задают не мнимый, а касающийся пучок окружностей, касающихся А в точке Р).
Мы считаем все окружности, проходящие через данную точку – ортогональными ей. В этом случае мы можем определить пучок окружностей, ортогональный двум точкам – это пучок проходящих через них окружностей. Пучок, ортогональный точке Р и окружности А – это пучок окружностей, проходящих через Р и ортогональных А. Это равносильно тому, что окружности проходят через А и А(Р).
В первой части мы утверждали, что для любых трех инверсий (или точек), существует инверсия, коммутирующая (ортогональная) им. Докажем это. Разберем сперва случай, когда среди трех данных инверсий (точек) есть точки. Трем точкам ортогональна окружность, проходящая через них. Паре точек Р и Q и инверсии А ортогональна окружность, проходящая через Р, Q, A(P) и А(Q). Точке Р и инверсиям А и В ортогональна окружность, проходящая через Р, А(Р), В(Р). Пусть теперь А, В, С – инверсии, действительные или мнимые. Покажем, что существует инверсия (действительная или мнимая), коммутирующая с ними всеми или – эти окружности пересекаются в одной точке. В этом случае мы говорим, что эта точка и ортогональна им всем.
Три инверсии А, В, С образуют три пучка (А, В), (В, С), (А, С). Если среди них есть хоть один мнимый пучок, то проведем окружность через центры этого пучка и ортогональную третьей инверсии. Она и даст искомую инверсию. Если среди этих пучков нет мнимых, значит все инверсии А, В, С, – действительны (т.к. мнимые инверсии входят только в мнимые пучки), и все неподвижные окружности этих инверсий имеют общие точки (пересекаются или касаются). А этот случай мы уже рассматривали (ст. 2, теорема о пучках и построение инверсии по образам двух точек или по тройке пересекающихся окружностей).

Пучки, тождество (А*В*С)2=e и непрерывность.


Заметим еще одно свойство пучков. Пусть у нас есть две произвольные окружности А и В. Тогда А(В) и В(А) – лежат в пучке, образованном А и В. Также и биссектрисы между А и В лежат в этом пучке. Таким образом, зная две окружности пучка, мы можем получить множество других окружностей с помощью инверсии, их композиций и проведения биссектрис. Рассмотрим подробней композицию инверсий: А, В, А(В), В(А), В(А(В), А(В(А)), В(А(В(А))),… Удобно выделить два преобразования f1=А*В и f2=В*А (легко видеть, что они взаимнообратные, их композиция – тождественное движение: f1*f2=(А*В)*(В*А)=А*(В*В)*А=е т.к. А и В – инволютивны, А*А=В*В=е) и рассмотреть последовательные действия:

f1(A), f1(f1(A)),… f1k(A)…
f2(B), f2(f2(B)),… f2k(B)…
Мы видим, что если пучок мнимый (А и В не имеют общих точек), то результаты этих композиций будут стягиваться к центрам пучка. В первом ряде к одному, во втором – к другому. f1 «тащит» окружность (и все точки плоскости) в одном направлении, f2 – в противоположном.
Если пучок (А, В) – касающийся, то оба ряда будут стягиваться к единственному центру пучка (но и «вытягиваться» оттуда), но стягиваться по разным направлениям. Если (А, В) – действительный пучок, то окружности будут «поворачиваться), возможно при каком-нибудь К f1k(A)=A, f2k(В)=В (все вернется на свои места, как при вращении прямых). Если А и В очень близки друг к другу, то f1=А*В и f2=В*А оба изменяют все не очень сильно. Тогда f1(A) близко к А, последовательно применяя f1 к А мы будем иметь плавное изменение окружности А. Если же будем применять f2 к А, то получим плавное изменение А «в другую сторону». Мы можем мыслить пучок окружностей, как результат плавного изменения окружностей. Особенно наглядно это в случае мнимого пучка: окружность постепенно разрастается из одного центра пучка, дорастает до прямой и сжимается во втором центре пучка.
Вернемся к тождеству (А*В*С)2=е, оно утверждает, что композиция трех инверсий из одного пучка – инволютивна. На самом же деле – не только инволютивна, но и есть инверсия относительно окружности из этого пучка. Если С можно получить применяя инверсии А и В (как мы проделывали ранее), то требуемое нетрудно показать алгебраически. Более того, если с помощью неких окружностей P и Q можно композициями инверсий относительно их самих можно выразить А, В, С, то опять-таки требуемое получается очень просто. (Мы рассмотрим это в ст. 5). Но это можно сделать не всегда, подобно тому, как существуют несоизмеримые длины. Но, подобрав Р и Q достаточно близко друг к другу, мы сможем с помощью инверсий выразить произвольные окружности пучка, в котором лежат Р и Q – сколь угодно точно. Далее, с помощью стандартного предельного перехода можно видеть, что (А*В*С)2=е, раз А, В, С сколь угодно близки к инверсиям, для которых это тождество имеет место.
В этой статье мы не первый раз говорим о предельных переходах. Докажем по-новому, с помощью такого перехода, уже хорошо известный нам факт геометрии окружности. Доказательство интересно тем, что синтезирует в себе важные топологические и алгебраические идеи. Пусть есть две не имеющие общих точек окружности А и В.
Докажем, что всякая окружность, ортогональная им – проходит через центры пучка (А, В). Доказательство:
Пусть С – ортогональная им окружность. Тогда С ортогональна и А(В) и В(А(В)) и т.п. все окружностям из описанного выше ряда, т.к. инверсии относительно А и В оставляют С на месте и сохраняют ортогональность окружностей. Все ортогональные окружности – пересекаются. Значит С пересекается со всеми окружностями типа А(В), В(А(В)), А(В(А))… Но эти окружности стягиваются сколь угодно близко к центрам пучка. Если С не проходит через какой-то центр пучка, то какая-то окружность указанного ряда будет ближе к центру пучка, чем С и поэтому – не пересечется с С. Но это невозможно, т.к. все эти окружности – ортогональны С. Поэтому С проходит через оба центра пучка. Что и требовалось доказать.

В окончание статьи докажем, что тождество (А*В*С)2=е выполняется только в двух случаях.
1. А. В, С – в одном пучке.
2. Все А, В, С – ортогональны друг другу.
Для этого нам понадобится простая лемма (докажите ее самостоятельно): если композиция каких-то двух инверсий Р и Q переводит в себя какую-то пару точек (т.е. либо меняет местами две точки, либо оставляет обе неподвижными), то эта пара точек является центрами пучка, образованного инверсиями Р и Q.
Теперь мы докажем, что если (А*В*С)2=е, то А переводит в себя центры пучка, образованного В и С. Подсчитаем композицию А(В(С(А(В(С(Х)))))) если Х – один из центров пучка (В, С). А(В(С(центры пучка (В, С))))=А(центры пучка (В, С)) (т.к. В и С переводят в себя центры образованного ими пучка). Применим еще раз А*В*С: А(В(С(А(центры пучка (В, С))))=(центры пучка (В, С)) т.к. по предположению А*В*С примененное дважды возвращает все точки на свои места, в том числе и центры пучка (В, С). Применим инверсию А к левой и правой части, получим В(С(А(центры пучка (В, С)))=А(центры пучка (В, С)). Значит В*С переводит пару точек А(центры пучка (В, С)) в ту же пару точек. По лемме отсюда следует, что А(центры пучка (В, С))=(центры пучка (В, С)). Это и означает, что А переводит центры пучка (В, С) в себя. Разобрав все варианты видим, что это означает, что либо А лежит в пучке (В, С) или А ортогональна В и С. В первом случае мы имеем требуемое, это случай 1. Во втором случае – А коммутирует с В и С. Воспользуемся этим: (А*В*С)2=А*В*С*А*В*С=В*С*А*А*В*С=В*С*В*С=е (сначала мы воспользовались, что А коммутирует с В и С, затем, что А*А=е). Но В*С*В*С=е равносильно тому, В*С=С*В (домножив обе части на С*В). Это и означает, что В и С коммутируют между собой или ортогональны. что и требовалось. Случай, когда В и С касаются – предлагаю разобрать самостоятельно.
Используются технологии uCoz