Статья 6.

Наглядные теоремы и построения. (Возвращение к старым темам).

Краткое содержание статьи.

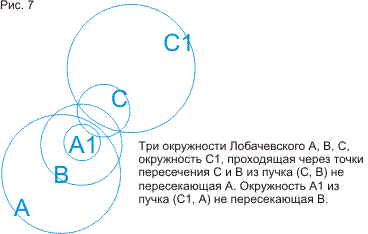
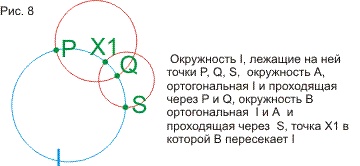
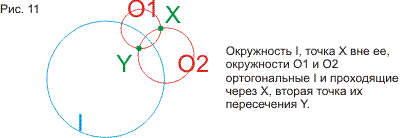
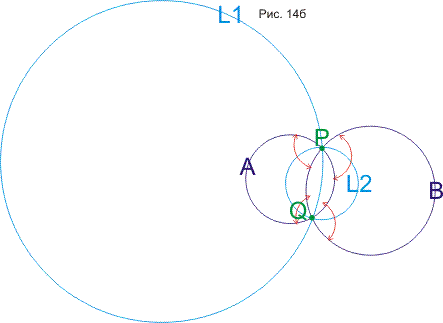
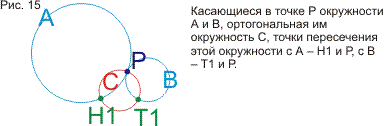
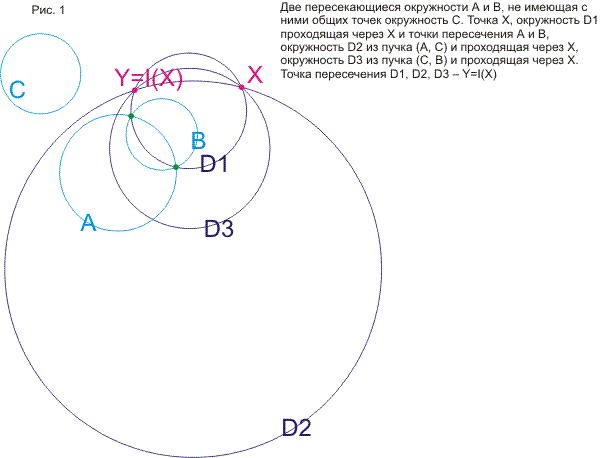
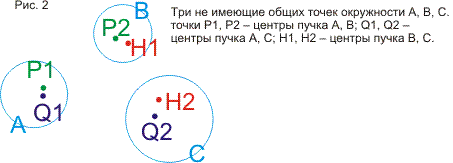
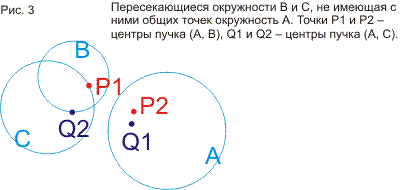
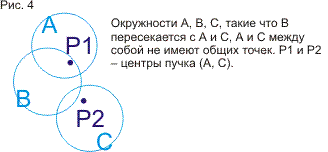
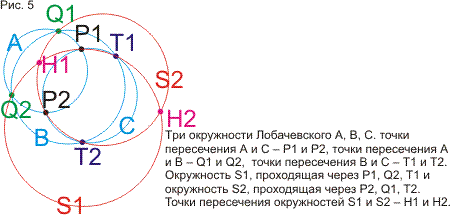
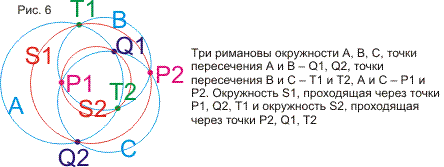
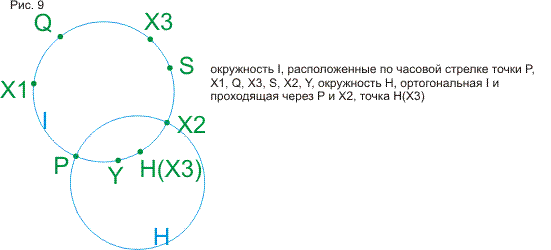
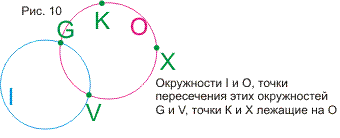
В этой статье обсуждаются темы, появлявшиеся в предыдущих статьях. Сначала указываются разные способы построения окружности, ортогональной трем данным и доказываются теоремы про окружности, построенные на точках пересечения трех данных окружностей. Затем доказывается сформулированное в ст.3 утверждение, что отображение плоскости, отображающее окружности в окружности и неподвижное в трех точках – либо инверсия, либо тождественное движение. 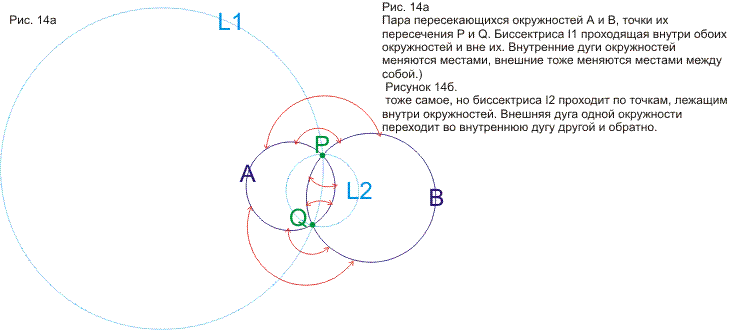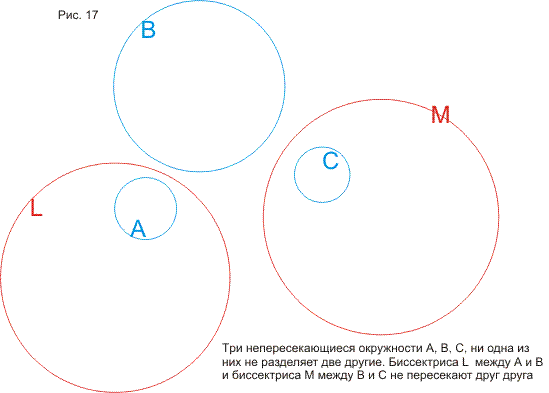Наконец, изучаются новые свойства биссектрис окружностей и я возвращаюсь к задаче Аполлония.

Окружность, ортогональная трем данным.


В статьях 4 и 5 мы многократно использовали тот факт, что для трех инверсий А, В, С существует одна, коммутирующая с ними всеми. Для доказательства мы использовали теорему о пучках (ст. 2). Сейчас я это кратко повторю, сейчас я это кратко повторю, ограничиваясь тем случаем, когда все три инверсии – действительные, т.е. имеют неподвижную окружность.
Пусть, например, А, пересекается с В но они обе не имеют общих точек с С. Возьмем произвольную точку Х и построим ее образ I(X), где I – коммутирующее с А. В, С отображение.


По теореме о пучках D1, D2, D3 все проходят через какую-то точку Y которая и будет образом X при инверсии, коммутирующей с инверсиями относительно А, В, С. Но как нарисовать эту инверсию? Точнее, как найти ее неподвижную окружность (существующую, если инверсия действительная)? Без этого инверсия кажется какой-то слишком абстрактной. Решение зависит от взаимного расположения окружностей А, В, С.
1. Окружности А, В, С – не пересекаются.


Докажем, что все шесть центров пучков (образованных исходными окружностями А, В, С) – лежат на одной окружности I, которая и будет ортогональна (коммутирующей) с А, В, С. Проведем окружность I через два центра одного пучка, например (А, В) – Р1 и Р2 и один из центров пучка (А, С), Q1. Мы можем это сделать, т.к. через три точки всегда можно провести окружность. Т.к. I проходит через пару сопряженных относительно А точек Р1 и Р2 то I ортогональна А, т.к Р1 и Р2 сопряжены и относительно В, то I ортогональна и В. Докажем, что I ортогональна и С. Т.к. I проходит через Q1 и А(Q1)=Q2, то I проходит и через Q2. Но раз I проходит через пару сопряженных относительно С точек Q1 и Q2 то I ортогональна и С. Т.к. I ортогональна В и С, то она проходит через центры пучка (В, С) H1 и H2. Что и требовалось, мы доказали, что I проходит через все шесть центров пучков и что она ортогональна А, В, С.
2. Пусть А не пересекается с В и С, а В и С – пересекаются между собой.


Т.к. А(Р1)=Р2, А(Q1)=Q2, то через эти четыре точки можно провести окружность. Она и будет ортогональна А, В, С.
3. А не пересекается с С, остальные окружности пересекаются.


Инвертируем точки Р1 и Р2 относительно В и проведем через четыре точки Р1, Р2, В(Р1), В(Р2) окружность I. Т.к. она проходит через Р1 и Р2, то она ортогональна А и С, а т.к. она проходит через Р1 и В(Р1) – она ортогональна В. Что и требовалось.
Наиболее интересны варианты, когда все окружности А, В, С – пересекаются между собой. в этом случае возможно следующее:
А. Ни одна из окружностей не разделяет точки пересечения двух других. По причинам, которые станут понятны в следующих статьях я называю такой случай расположения окружностей А, В, С – случаем Лобачевского, а сами три окружности – окружностями Лобачевского.
В. Все три окружности А, В, С пересекаются в одной точке. Я называю этот вариант расположения окружностей – евклидовым. В этом случае нет необходимой инверсии, коммутирующей с А, В, С (если не считать, как было сделано в ст. 4 таковой – отображение всей плоскости в их точку пересечения). Предлагаю самостоятельно провести рассуждения аналогичные рис. 1.
С. Одна из окружностей разделяет точки пересечения двух других. Предлагаю самостоятельно доказать, что в этом случае и любая другая окружность разделяет точки пересечения двух оставшихся. Я называю такой случай расположения окружностей А, В, С Римановым, а сами окружности – Римановыми.

Три окружности Лобачевского.


Рассмотрим случай А. Пусть есть три окружности Лобачевского.


Мы будем строить окружности, проходящие через одну из точек, каждой из трех пар точек пересечения окружностей между собой. Поскольку в каждой паре – две точки пересечения, а всего пар три, то всего таких окружностей 2х2х2=8. Эти восемь окружностей можно разбить естественным образом на пары, следующим образом. Выберем из трех двоек точек по одной точке., проведем через выбранные три точки окружность. Теперь возьмем оставшиеся три точки и проведем другую окружность. Она и будет парной к первой. Таким образом мы разбиваем 8 окружностей на четыре пары окружностей. На рис. 5 изображены две парные окружности: S1 и S2. S1 проходит через P1, Q2, T1, а S2 через оставшиеся точки – P2, Q1, T2.
Среди этих четырех пар окружностей может быть одна пара – непересекающихся (доказательство, что такая пара может быть только одна не сложно, но ради экономии места я здесь не буду его приводить, предлагаю сделать это самостоятельно и позже). Если она есть, мы ее не будем рассматривать. Таким образом у нас останется три пары пересекающихся окружностей. Пусть S1 и S2 – пересекаются. Обозначим точки их пересечения Н1 и Н2. Аналогично мы получим точки пересечения двух других пар окружностей, обозначим их H3, H4, H5, H6.
Теорема об ортогональной окружности к трем окружностям Лобачевского утверждает, что все эти шесть точек: Н1, Н2, Н3, Н4, Н5, Н6 – лежат на одной окружности I и эта окружность – ортогональна А, В, С. Также эту теорему можно назвать «Теоремой об описанных окружностях трехокружника Лобачевского» (назвав, по аналогии с треугольником, окружности, проходящие через точки пересечения трех данных, – «описанными окружностями»).
Доказательство. Из теоремы о пучках (ст. 2) мы знаем, что инверсия I, меняющая местами пары точек пересечения окружностей А, В, С – существует. I(P1)=P2, I(Q1)=Q2, I(T1)=T2. Из этого следует, что I(S1)=S2. И точно также – парные окружности, построенные на точках пересечения А, В, С – меняются местами под действием I. Теперь докажем лемму:
Если окружности F и G сопряжены инверсией O и пересекаются, то, если O – действительная инверсия, то точки пересечения остаются неподвижными, под действием О (лежат на О). Если О – мнимая инверсия, то… Мы выясним, что будет по ходу дела.
Доказательство тривиально. Т.к. O(F)=G, то точки пересечения F и G снова переходят в точки пересечения F и G. Т.к. точек пересечения всего две, то они – либо обе неподвижны, либо меняются местами. Рассмотрим сначала случай, когда О – действительная инверсия. Если пара точек пересечения F и G меняется местами под действием О, то все окружности, проходящие через эту пару – ортогональны О и при инверсии относительно О – останутся перейдут в себя. Но, по условию O(F)=G и F не совпадает c G. Следовательно, точки пересечения F и G не меняются местами под действием инверсии относительно О. Следовательно эти точки пересечения остаются неподвижны и поэтому лежат на О. Что и требовалось.
Пусть О – мнимая инверсия. Т.к. у мнимой инверсии нет неподвижных точек, то точки пересечения F и G – меняются местами. Но, применяя тоже самое рассуждения, что и для случая когда О – действительная инверсия, получим, что F и G – должны быть ортогональны О. Но этого не может быть, т.к. O(F)=G. Где же выход? Решение в том, что мы попутно доказали, что при мнимой инверсии образ окружности и ее прообраз не могут пересекаться (но могут совпадать)! (В противном случае получается противоречие: точки пересечения не могут ни быть неподвижными, не могут и поменяться местами. Значит этих точек просто нет.)
Вернемся к трем окружностям Лобачевского, изображенным на рис. 5 и нашей теореме. Применим лемму, получим: Н1, Н2 лежат на окружности I, ортогональной А, В, С, точно также и Н3, Н4, Н5, Н6 – лежат на этой окружности. Т.к. все эти точки лежат на пересечении окружностей, меняющихся местами при инверсии относительно I. Что и требовалось.

Римановы окружности и евклидовы окружности.


Рассмотрим случай, когда три окружности А, В, С – римановы, т.е. одна из окружностей разделяет точки пересечения двух других.


Если в этом случае мы построим окружности на точках пересечения А с В, В с С, А с С аналогично тому, как это сделано на рис. 5 и разобьем, как и в предыдущем случае на пары, то ни одна окружность не пересечется с парной ей. Это прямо следует из того, что инверсия I, коммутирующая с А. В, С и меняющая местами точки пересечения: I(P1)=P2, I(Q1)=Q2, I(T1)=T2 – мнимая (см. ст. 2 или ст. 3) и приведенной ранее леммы о том, что окружности, сопряженные относительно мнимой инверсии – не могут пересекаться.
Мы можем найти центр и радиус этой мнимой инверсии I. Центр – как точку пересечения прямых (Р1, Р2) и (Q1, Q2) и (T1, T2), радиус – исходя из определения инверсии через длины. (см. ст. 2).
Если же три окружности А, В, С – евклидовы, т.е. все проходят через одну точку, то не существует инверсии (действительной или мнимой) коммутирующей с А, В и С. Это можно доказать, например, осуществив инверсию с центром в этой общей точке. Тогда три окружности перейдут в прямые. Предлагаю доказать самостоятельно, что для трех прямых в общем случае не существует окружности, ортогональной им всем. Заметим одно исключение: если все три окружности имеют не одну, а целых две общие точки – то, разумеется есть бесчисленное количество ортогональных им окружностей.
Обратим внимание на следующее: случай евклидового расположения окружностей можно воспринимать как результат предельного перехода из Риманова или Лобачевского случая. Или, как пограничный между этими двумя случай.

Новые свойства трех окружностей.


Если мы проведем окружность D через общую точку пересечения трех евклидовых окружностей А, В, С, то она, очевидно, вместе с любыми двумя окружностями из А, В, С – снова образует «Евклидов трехокружник». Если же мы проведем окружность D через пару точек пересечения двух римановых окружностей (например, через пересечение А и В), то трехокружники В, С, D и А, D, С – снова будут римановыми (например, потому, что D ортогональна мнимой инверсии I, ортогональной А, В, С, т.к. D проходит через пару сопряженных этой инверсией точек). Мы можем провести новую окружность D1 через пару точек пересечения каких-либо двух из уже четырех имеющихся окружностей, она, в совокупности с двумя другими – снова образует трехокружник Римана (или эти три окружности образуют один пучок). Так мы получаем семейство окружностей любые три из которого (не лежащие в одном пучке) – образуют трехокружник Римана. И все окружности семейства – ортогональны одной и той же мнимой инверсии I.
Если называть «трехокружником Лобачевского» и тройки окружностей, где могут быть и две касающиеся друг друга или вовсе не пересекающиеся (это логично, т.к. в этом случае третья окружность никак не может разделить «точки пересечения двух других») – то аналогичное свойство обнаруживается и у трех окружностей Лобачевского. Если провести окружности D, D1, D2, D3… через пары точек пересечения окружностей Лобачевского, то получаем семейство окружностей, любые три из которого образуют трехокружник Лобачевского. И, разумеется, все они ортогональны действительной инверсии I.
Заметим еще, что если А, В, С – ортогональны некоторой окружности I (действительной или мнимой), то А(В), А(С), В(С) и все дальнейшие окружности, получаемые инверсиями из трех данных – снова будут ортогональны относительно I. Также, если воспользоваться терминами статьи 5, можно сформулировать: преобразования, полученные композициями инверсий коммутирующих с данной I – образуют подгруппу в группе всех преобразований плоской геометрии окружности.

Трехмерное обобщение теоремы о трехокружнике Лобачевского.


Здесь я только намечу трехмерное обобщение этой теоремы. Пусть даны четыре сферы А, В, С, D, такие, что любые три из них – пересекаются в двух точках, а четвертая не разделяет эти точки пересечения. Каждые три сферы из этих четырех имеют две точки пересечения. Всего имеется 4 тройки сфер: А, В, С; А, В, D; А, С, D; В, С, D; и, соответственно – 4 пары точек пересечения. Точно также, как в плоском случае – имеется инверсия I, отображающая каждую из сфер А, В, С, D в себя и меняющая местами точки в каждой паре пересечения.
Выберем из каждой пары точек пересечения про точке и проведем через них сферу S1 (всего окажется выбранными 4 точки, а через четыре точки всегда можно провести сферу), а через оставшиеся четыре точки – сферу S2. Если сферы S1 и S2 пересекаются (или касаются) – все их общие точки (окружность или точка) – остаются неподвижными при инверсии I. Это доказывается точно также, как и в плоском случае: Сфера, на которой лежит пара сопряженных точек, переходит в себя при инверсии относительно сопрягающей сферы, но I(S1)=S2 S1 не совпадает с S2, значит ни на S1. ни на S2 нет сопряженных точек, значит, каждая точка пересечения S1 и S2 – остается неподвижной при инверсии I. Значит, окружность, по которой пересекаются S1 и S2 – лежит на I. Всего мы имеем четыре пары точек пересечения, выбирая из каждой пары по одной точке имеем 2х2х2х2=16 сфер, которые группируем, так же как и в плоском случае на 8 пар (в одной паре лежит сфера проведенная через четыре произвольно выбранные точки и сфера, проведенная через оставшиеся четыре точки). Окружности пересечения каждой пары сфер лежат на одной сфере I. Заметим, что некоторые пары сфер из восьми рассмотренных пар могут не пересекаться.

Еще один способ построения окружности, ортогональной
трем окружностям Лобачевского.


Вернемся к плоскости и укажем еще один способ построения окружности, ортогональной трем данным. Пусть у нас есть три окружности Лобачевского А, В, С.


Окружности А, В, С и А, В, С1 ортогональны одной и той же окружности I (т.к. окружность ортогональная С и В ортогональна и С1). Также и окружности А1, С1, В – ортогональны I, т.к. А1 ортогональна окружности, ортогональной С1 и А, а это – I. Но среди окружностей А1, С1, В – нет пересекающихся! Поэтому, достаточно найти центры пучков (А1, С1) и (А1, В) и провести через них окружность – она и будет искомой (как было показано ранее, на ней будут лежать и центры пучка (С1, В)).
Центры пучка можно найти двумя способами.
1. Провести пару окружностей, ортогональных к двум окружностям пучка. Точки их пересечения и будут центрами пучка.
2. Начать данные окружности друг в друга. Они начнут стягиваться к центрам пучка, постепенно образы окружностей будут неотличимы от точек.
Из-за п. 2 мы можем просто начать инвертировать окружности А1, С1, В друг в друга и, когда образы станут очень малы, – провести через них окружность, которая будет практически неотличима от ортогональной трем исходным окружности I. Замечу, что с некоторыми небольшими модификациями этот способ (инвертировать окружности друг в друга, пока не «стянутся к точке») – годится и для трех исходных А, В, С. Какие именно нужны модификации я сейчас не будут касаться, замечу лишь, что если рассмотреть композицию h=А*В*С, то она постепенно стягивает все точки плоскости к точке, лежащей на окружности I, т.е. последовательность Х, h(X), h(h(X))… hn(X)… стремится к некоторой одной точке на окружности I, какова бы ни была исходная точка Х. (Если А, В, С – римановы окружности, то ничего похожего не происходит).

Теорема о трех неподвижных точках.


Сейчас мы восполним один очень важный пробел. В статье 3 я без доказательства утверждал, что если у нас есть преобразование, полученное композицией инверсий и у него есть три неподвижные точки, то это преобразование – инверсия или тождественное движение. Сейчас я это докажу.
Обозначим эти неподвижные точки P, Q, S и проведем через них окружность I. Сначала я докажу, что всякая точка окружности I остается неподвижной, если неподвижны P, Q, S. Обозначим наше преобразование точек f. Образ точки Х при преобразовании f это f(X). Т.к. f – композиция инверсий, то f отображает окружности в окружности и ортогональные окружности – в ортогональны окружности. Если точка Х лежит на одной окружности с P, Q, S то и f(X) лежит на той же окружности, т.к. f(X), f(P), f(Q), f(S) должны снова быть на одной окружности, но f(P)=P, f(Q)=Q, f(S)=S по условию, то это окружность I. Теперь я покажу, как построить, исходя из трех данных точек P, Q, S бесчисленное множество других точек, лежащих на I и также остающихся неподвижными при действии f. Проведем через Р и Q окружность А ортогональную I. f(A) – снова окружность, причем она будет ортогональна I (т.к. f(I)=I) и проходящая через Р и Q (т.к. f(P)=P, f(Q)=Q). Такая окружность единственна, значит f(A)=A, т.е. А переходит в себя под действием f (но точки А могут меняться местами!). Теперь проведем через S окружность В, ортогональную I и А. Опять-таки – такая окружность единственна и т.к. f(I)=I и f(A)=A, то f(B)=B, она переходит в себя под действием f. Окружность В пересекается с I в какой-то точке X1 (и, разумеется, в точке S). Покажем, что точка Х1 будет неподвижна под действием f, f(X1)=X1. Т.к. f(I)=I f(B)=B то точки пересечения I и B переходят в себя под действием f. Но одна из этих точек, S – неподвижна по условию. Значит и вторая, Х1 – также неподвижна (ей просто некуда больше переходить). итак, мы доказали, что если есть три неподвижные точки, P, Q, S, то есть и четвертая неподвижная точка Х1, лежащая на I.


Заметим, что из статьи 5 следует, что Х1 это точка, симметричная S относительно биплета (пары точек) P и Q, также X1=A(S).
Теперь мы можем построить аналогично пятую, шестую и т.п. неподвижные точки (все они будут лежать на I). проведем окружность, ортогональную I не через Р и Q, а через Р и S и инвертируем относительно нее Q – получим X2, еще одну неподвижную точку, инвертируем Р относительно окружности, ортогональной I и проходящей через Q и S – получим Х3, также неподвижную под действием f. Мы можем выбрать любую пару неподвижных точек, а их уже шесть, инвертировать какую-нибудь из них относительно окружности, ортогональной I и проходящей через любую пару неподвижных точек и получить новую неподвижную точку.
Докажем, что к любой точке Y на окружности I можно сколь угодно близко подойти по неподвижным точкам (получаемым описанным выше способом).


Выберем среди неподвижных точек пару таких, что между ними и Y еще нет неподвижных точек. На рис. 9 это точки Х2 и Р. Найдем точку по другую сторону дуги (Х2, Р) (ту сторону, где нет Y) неподвижную точку «подальше» от X2 и Р, например Х3. Проведем окружность Н через Х2 и Р ортогональную I и инвертируем относительно нее Х3. Н(Х3) – снова будет неподвижной точкой и лежит по ту же сторону от Х2 и Р что и Y. Теперь выберем среди трех точек Х2, Н(Х3), Р пару точек, между которыми лежит Y и сделаем с этой парой тоже самое – проведем через нее ортогональную I окружность, найдем неподвижную точку «подальше» от Y, инвертируем ее относительно проведенной окружности и так далее. На каждом этапе мы будем окружать Y все более близкими парами неподвижных точек. Что и требовалось.
Чтобы ускорить процесс, мы можем инвертировать относительно Н все точки, лежащие по другую сторону дуги (Х2, Y, P). Среди полученных образов выбрать пару, между которой лежит Y, а неподвижных точек – не существует. Построить ортогональную к I окружность, проходящую через эту пару, инвертировать все неподвижные точки относительно этой окружности и т.п.
Итак, мы показали, что сколь угодно близко к любой точке Y окружности I – есть неподвижные точки. Поскольку f – непрерывна, т.е. отображает близкие друг к другу точки снова в близкие друг к другу точки, то f(Y)=Y т.е. Y – тоже неподвижная точка отображения f. Значит, все точки окружности I остаются неподвижными под действием f. Покажем теперь, что если есть еще хоть одна неподвижная точка К вне I, то f – тождественное движение (т.е. неподвижна на всех точках плоскости).


Пусть Х – произвольная точка плоскости, проведем через К и Х какую-нибудь окружность О, пересекающую I. Пусть F и V – точки пересечения. Они лежат на I, следовательно – неподвижны при действии f. Значит, на окружности О есть три неподвижные точки К, G и V. Но, мы показали, что если есть три неподвижные точки, то все точки на окружности, проходящей через эти три точки – неподвижны, значит и Х, лежащая на той же окружности, что К, G и V – неподвижна. при действии f. Что и требовалось.
Теперь докажем требуемое. Что f – или инверсия, или тождественное преобразование. Проведем через Х пару каких-нибудь окружностей О1 и О2, ортогональных I. f(O1)=O1, f(O2)=O2 (т.к. точки пересечения О1 и О2 с I – неподвижны и ортогональные окружности под действием f переходят в ортогональные окружности). Значит, точки пересечения О1 и О2 (одна из них Х) – либо меняются местами, либо остаются неподвижны. Если f(X)=X, то, по доказанному ранее, f – тождественное движение. Пусть f отображает Х во вторую точку пересечения О1 и О2.


Вторая точка пересечения О1 и О2 и есть образ точки Х при инверсии относительно I. Значит, для произвольной точки Х f(X)=I(X). Что и требовалось: f – либо инверсия, либо тождественное движение.
Проанализируем и усовершенствуем доказанное. Мы доказали, что всякое взаимнооднозначное непрерывное отображение плоскости в себя, сохраняющее окружности (отображающее окружности в окружности) и отображающее ортогональные окружности в ортогональные имеющее три неподвижные точки – либо инверсия, либо тождественное движение. Сейчас я докажу, что в этой формулировке есть тавтология. Было сказано «…отображение, сохраняющее окружности и отображающее ортогональные окружности в ортогональные…» Я докажу, что всякое взаимно-однозначное отображение f, отображающее окружности в окружности – отображает ортогональные окружности в ортогональные. Доказательство, пожалуй, проще, чем сама формулировка. (Заметим, что аналогичное утверждение про прямые не плоскости неверно. Например, сжатие плоскости по одной из осей координат – отображает прямые в прямые, но перпендикулярные прямые перестают быть перпендикулярны).
В ст. 3 мы показали, что окружности, проходящие через три точки пересечения трех взаимнокасающихся окружностей – ортогональна им всем. Также было доказано, что если две ортогональные окружности А и В пересекаются в точках P и Q, то какие бы окружности С и D, касающиеся В в точках Р и Q мы не провели – если С и D касаются друг друга, то точка их касания лежит на А.


Теперь докажем требуемое. Пусть А и В – ортогональные окружности, Р и Q – точки их пересечения. Нам требуется доказать, что f(A) и f(B) ортогональны. Проведем еще окружности С и D , касающиеся В в точках Р и Q. Пусть C и D касаются друг друга в точке Н, лежащей на А. Рассмотрим f(A), f(B), f(C), f(D). Т.к. f переводит окружности в окружности и взаимно однозначно – f отображает касающиеся окружности в касающиеся окружности. Значит f(B), f(C), f(D) – снова тройка взаимнокасающихся окружностей. Т.к. А проходит через точки касания В, С, D, то f(A) проходит через точки касания f(B), f(C), f(D). Следовательно, f(A) – ортогональна всем трем окружностям: f(B), f(C), f(D). В том числе и f(B) – что и требовалось доказать.
Подведем итог. Мы доказали, что если непрерывное взаимнооднозначное отображение f отображает окружности в окружности и неподвижно на трех точках, то f – или инверсия или тождественное движение.
Необходимо уточненить про непрерывность. Если мы рассматирваем инверсии на плоскости, то, как было сказано, центр окружности, относительно которой осуществляется инверсия – переходит в бесконечно удаленную точку. Это создает разрыв отображения: точки, близкие к центру инверсии переходят в далекие друг от друга точки. Мы можем выйти из этого затруднения двояко: рассматривать все наши построения не на плоскости, а на сфере, а там инверсии и их композиции – будут непрерывны во всех точках. Либо заметить, что разрыв в одной точке не повлияет кардинально на наши рассуждения. Есть и третий способ рассуждения, «спасающий» доказательство: последовательность точек, стремящаяся к центру инверсии – перейдет в последовательность точек стремящуюся к бесконечно удаленной точке и тем самым непрерывность будет сохранена. Но этот способ требует слишком большого вторжения анализа в наши геометрические рассуждения.

Биссектрисы или серединные окружности.


Уже в первой статье про задачу Аполлония важнейшую роль играли биссектрисы, т.е. такие инверсии, которые сопрягают две данные окружности. О них говорилось и в других статьях, например, в ст. 3. Как само собой разумеющееся я упоминал, что биссектриса между А и В (действительная или мнимая) лежит в одном пучке с А и В. Сейчас я это докажу и найду другие свойства биссектрис.
Если А и В касаются или пересекаются, то что их биссектриса I лежит в одном с ними пучке – геометрически очевидно. Предлагаю доказать самостоятельно. Пусть А и В не имеют общих точек, т.е. образуют мнимый пучок. Покажем, что их биссектриса I отображает центры пучка (А, В) снова в центры пучка (А, В). В самом деле, эти центры сопряжены относительно А, значит их образ при инверсии относительно I сопряжен с I(A)=B. Но эти же центры сопряжены и относительно В, значит образ этих центров при инверсии относительно I сопряжен с I(B)=A. Поэтому образ этих центров сопряжен и относительно А и относительно В. Но у нас имеется только одна пара таких точек – это исходные центры пучка. Значит I отображает эту пару в себя. Если I оставляет каждый центр пучка неподвижным, то I будет ортогональна А и В, следовательно – не будет их биссектрисой. Значит I – меняет местами центры пучка А и В. Значит, по определению мнимого пучка – I лежит в пучке (A, B). Что и требовалось. Отсюда следует, что I ортогональна всем окружностям, ортогональным А и В. Это сразу позволяет нам понять, как I действует на точки.


Как было доказано, раз с С ортогональна А и В, то с ортогональна и I. I(C)=C, значит точки пересечения С и А перейдут под действием I в точки пересечения С и В. Возможны два варианта:
1. I(H1)=T1, I(H2)=T2. 2. I(H1)=T2, I(H2)=T1.
Рассмотрим первый случай. Как было показано в ст. 2 – инверсия полностью задается образами двух точек, мы можем найти центр инверсии как пересечение прямых (Н2, Т2) и (Н1, Т1). Но обычно нам нет необходимости искать центр. Зная образы двух точек мы. как описано в ст. 2 найдем образ любой третьей точки. Заметим, что пара точек Н1, I(H1)=T1 не разделяет пару точек Н2, I(H2)=T2, точка пересечения прямых, проходящих через эти пары – не разделяет эти точки, поэтому в этом случае мы имеем действительную инверсию.
Во втором случае пара точек Н1, I(H1)=T2 разделяет пару точек H2, I(H2)=T1, а точка пересечения прямых, проходящих через эти пары – разделяет точки пары, поэтому I – мнимая инверсия, у нее нет неподвижной окружности.
Если А и В пересекаются:


Заметим, что сейчас ни пара точек Н1, T1 не разделяет пару Н2, Т2, ни пара Н1, Т2 не разделяет пару Н2, Т1. Рассуждая аналогично предыдущему случаю мы получим, что или I(H1)=T1, I(H2)=T2 или I(H1)=T2, I(H2)=T1. Но, в отличие от предыдущего случая в обоих вариантах I будет действительной инверсией (т.к. пары точек: образ-прообраз не разделяют друг друга).






Т.к. I(P)=P, то возможен только один вариант I(H1)=T1. инверсия I однозначно определена. Мы можем провести еще С1, ортогональную А и В и получить в точках ее пересечения с А и В еще пару точек, сопряженную относительно I.
Итак, мы доказали, что:
1. У двух пересекающихся окружностей есть две действительные биссектрисы.
2. У окружностей, не имеющих общих точек, также есть две биссектрисы. Одна – действительная, другая – мнимая. Мнимая инверсия отображает точки с окружности А на окружность В как бы «крест-накрест».
3. В обоих случаях обе биссектрисы – коммутируют друг с другом (см. ст.3).
4. Если окружности касаются – есть только одна биссектриса между ними. (этот случай можно рассматривать как переходный между пересекающимися и не пересекающимися окружностями. Точки пересечения расположены «очень близко» друг к другу.)
Как построить окружность I?
Мы показали, как определить образ произвольной точки Х на А при инверсии I. Достаточно провести ортогональную к А и В окружность С через точку Х. (для этого можно инвертировать Х относительно В, полученное инвертировать относительно А и через три точки провести окружность, она будет ортогональна А и В и проходит через Х). Чтобы выбрать, какая из двух точек пересечения В с С будет I(X) – надо знать, какая из двух возможных биссектрис нам нужна. Пусть мы это знаем. Тогда возьмем на окружности А три точки Х1, Х2, Х3 и найдем указанным способом их образы I(X1), I(X2), I(X3). А если мы знаем образы трех точек при действительной инверсии мы легко можем построить и окружность инверсии, например, с помощью теоремы о трех окружностях Лобачевского. Три окружности Лобачевского в данном случае это окружности проходящие через:
1. X1, X2, I(X1), I(X2)
2. X2, X3, I(X2), I(X3)
3. X1, X3, I(X1), I(X3)
Мы строим окружности на точках пересечения этих трех окружностей, как было описано в названной теореме: окружности, проходящие через точки X1, X2, I(X3) и I(X1), I(X2), X3 – пересекаются в точках, лежащих на I, также окружности, проходящие через точки: X1, I(X2), X3 и I(X1), X2, I(X3) – пересекаются в точках, лежащих на I. Окружность, проведенная через эти точки пересечения и будет искомая I.
В случае, когда А и В имеют общие точки – есть и более простые способы построения биссектрисы, но здесь я не буду о них писать.

В статье. 5 была определена биплетная симметрия (симметрия относительно пары точек). Воспользуемся этим понятием, чтобы определить, чему равна композиция инверсий, относительно двух биссектрис между А и В. Пусть I1(A)=B и I2(A)=B. Ясно, что I1*I2(A)=A, I1*I2(B)=B. Т.к. I1 и I2 – коммутируют, то I1*I2 – биплетная симметрия. Концы этого биплета – центры пучка (А, В). Если А и В пересекаются, то концы биплета – точки их пересечения, это аналогично тому, что композиция симметрий относительно двух биссектрис между прямыми – симметрия относительно точки их пересечения. А если А и В не имеют общих точек, то концы этого биплета – центры мнимого пучка А и В. Они сопряжены и относительно А и относительно В.

Снова задача Аполлония.


Вернемся к задаче Аполлония о нахождении окружностей, касающихся трех данных. Напомним вкратце проведенное в ст. 1 построение.
1. Были проведены биссектрисы между окружностями А, В, С
2. Декларировалось, что три биссектрисы пересекаются в двух точках (а случай, когда биссектрисы не пересекаются – вовсе не рассматривался).
3. Из точек пересечения биссектрис были проведены перпендикулярные к А, В, С окружности.
4. Из точек пересечения этих перпендикуляров с А, В, С выбиралось по точке и утверждалось, что окружность, проведенная через эти три точки – касается А, В и С.
Рисунок 16.
(Три окружности Римана А, В, С, биссектрисы между А и В, В и С и С и А пересекающиеся в двух точках и перпендикуляры из этих точек пересечения, точки пересечения и окружность, проходящая через них).
Этот метод всегда работает, если три исходные окружности – римановы, т.е. одна разделяет точки пересечения двух других. Тогда биссектрисы в самом деле обязательно пересекаются. Но как модифицировать его для случая, когда они не пересекаются. Например:


Тогда нам пригодится понятие пучка. Если биссектриса I1 между А и В не пересекается с биссектрисой К1 между В и С, то она все равно образует с К1 пучок окружностей. Теорема о биссектрисах утверждает, что одна из двух биссектрис между А и С – обязательно лежит в этом пучке. Мы докажем теорему о биссектрисах позднее. Если бы I1 и К1 пересекались, мы бы провели из точек пересечения окружности, перпендикулярные А, В и С. Это можно сформулировать более общим образом. Из пучка (I1, К1) выбираются инверсии, ортогональная (коммутирующие) с А, В или С. а этом можно сделать всегда, т.к. в любом пучке есть инверсия (действительная или мнимая), коммутирующая с данной – см. ст. 4. (Есть исключение, если данная окружность проходит через один из центров мнимого пучка).
Итак, мы разобрались с тем, что делать, если биссектрисы не пересекаются. Осталось доказать, что окружность, построенная указанным способом – в самом деле обязательно касается А, В, С. Сначала докажем, что эта построенная окружность – ортогональна биссектрисам I1 и К1 (между А и В и между В и С). I1(A)=B, K1(B)=C. Центры пучка (I1, K1) при симметрии относительно I1 перейдут в себя и сам пучок тоже, окружность пучка, ортогональная А – перейдет в окружность пучка, ортогональную В. Значит точки пересечения окружности этого пучка ортогональной А с А перейдут в точки пересечения окружности пучка, ортогональной В с В. Пусть точки пересечения перпендикуляра с А – А1 и А2, с В – В1 и В2. Значит I1(A1) равно или В1 или В2. Пусть это будет В1. Значит окружность, проходящая через А1 и В1 – ортогональна I1. Теперь рассмотрим действие К1 на В1 и В2. К1 опять-таки переводит пучок (I1, K1) в себя, а перпендикуляр с В в перпендикуляр в С (т.к. К1(В)=С). Пусть К1(В1)=С1. Тогда С1 – одна из точек пересечения перпендикуляра из пучка (I1, K1) к окружности С с С. Проведем окружность через А1, В1, С1. Она ортогональна I1 т.к. I1(A1)=B1, она ортогональна K1, т.к. K1(B1)=C1. Что и требовалось доказать.
Обозначим построенную окружность, проходящую через А1, В1, С1 буквой S. Заметим, что мы еще и указали как именно выбирать точки (из пар точек пересечения), чтобы провести окружность, касающуюся А, В, С. Первую точку можно выбрать произвольно, затем отразить ее относительно I1 и К1 и взять образы. (Оставшиеся точки дадут вторую окружность, касающуюся А, В, С). Докажем, что если построенная окружность Ы касается одной из трех окружностей А, В, С – например, В – то она касается и остальных двух. Это просто. Пусть S касается В, тогда I1(S) касается I1(B)=A, К1(S) касается К1(В)=С. Но I1(S)=K1(S)=S т.к. S ортогональна I1 и К1. Значит S касается А и С, что и требовалось доказать.
Чтобы доказать, что S – искомая окружность, касающаяся А, В и С необходимо доказать, что S – касается В (одной из трех данных окружностей). Это будет сделано в следующих статьях.
Используются технологии uCoz