Статья 7.

Моделирование геометрий Лобачевского, Евклида и Римана в геометрии окружности.

Краткое содержание статьи.

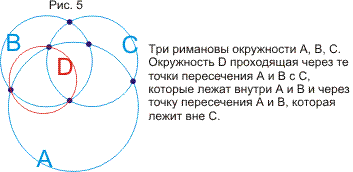
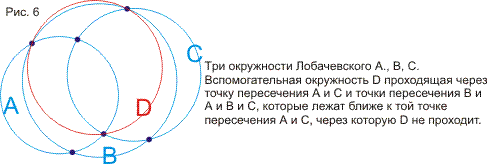
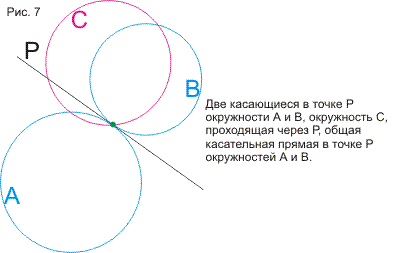
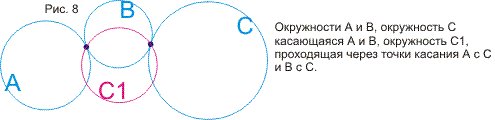
В статье излагаются две связанные между собой модели геометрий Евклида, Римана, Лобачевского. Первая модель – объемная. Представим себе, что Глаз в пространстве смотрит на сферу. А больше в пространстве совсем ничего нет. Если Глаз расположен вне сферы, то он увидит на сфере то, что подчиняется законам геометрии Лобачевского, если Глаз на поверхности сферы – он увидит геометрию Евклида, а внутри сферы – Римана.
Вторая модель – плоская, и как и в предыдущем случае, разные геометрии оказывается возможным изучать совместно, в рамках геометрии окружности. Доказывается теоремы о сумме углов треугольника в разных геометриях, о пересечении биссектрис треугольника и о равнобедренном треугольнике в разных геометриях.
Теоремы эти доказываются с помощью изучения углов между окружностями и понятия «изогональных окружностей» (Окружностей, образующих одинаковый угол с двумя данным окружностями). Теорема о биссектрисах в треугольниках разных геометрий оказывается частным случаем теоремы о биссектрисах между окружностями.
Перед прочтением этой статьи желательно, но не обязательно просмотреть ст.4 и ст.5. Объемная модель неевклидовых геометрий рассмотрена в моей статье в журнале «Математическое просвещение» (№3, 1999 год).


Объемная модель различных геометрий.


Для читателей, внимательно прочитавших ст. 4 и просмотревших статью 5, я бы начал просто: рассмотрим А-отображение с центром в О сферы S.
1. Если О расположено снаружи S, то подгруппа, порожденная А-отображениями, коммутирующими с А-отображением в центре О – изоморфна группе движений плоской геометрии Лобачевского. Пара точек (Х, О(Х)) называется точкой геометрии Лобачевского, а прямыми геометрии Лобачевского – окружности сферы S, лежащие в одной плоскости с О. При этом А-отображение, коммутирующее с О(Х) определяет точечную или осесимметрию геометрии Лобачевского. Центр такого А-отображения лежит на поляре Точки О. Обозначим центр этого отображения – В. Если В вне сферы, то В(Х) – определяет осесимметрию, а если внутри – точечную симметрию.
2. Если О расположено внутри сферы, то определение «точек и прямых римановой геометрии» будет таким же, как и пред. случае, подгруппа, порожденная А-отображениями, коммутирующими с О(Х) – изоморфна группе движений римановой геометрии. Всякая точка В, лежащая на поляре О определяет осесимметрию римановой геометрии. поляра О в этом случае целиком лежит вне S.
3. Если О лежит на сфере S, то рассмотрим отображение всей сферы S в одну точку О и совокупность А-отображений коммутирующих с этим отображением. Пара точек (Х, О(Х)) – определяет точку евклидовой геометрии, а окружности, проходящие через О (лежащие в одной плоскости с О) – называются прямыми евклидовой геометрии. Центры А-отображений, коммутирующих с О(Х) (О(Х)=О для всех Х) лежат в плоскости, касающейся S в точке О. Эти А-отображения порождают подгруппу, изоморфную группе движений Евклидовой геометрии и каждое из них определяет осесимметрию геометрии Евклида.

Но, поскольку я стараюсь сделать статьи не очень зависимыми друг от друга, то сейчас поясню описанные конструкции. Пусть О – произвольная точка трехмерного евклидова пространства. Назовем «связкой» – все плоскости и прямые, проходящие через О. Заметим, что любые две плоскости из связки пересекаются по некоторой прямой из связки. поместим теперь в пространство сферу S. Я назову «точкой» геометрии (не уточняя пока какой – евклидовой, римановой или Лобачевского) – прямую из связки, пересекающую сферу. «Прямой» геометрии (опять-таки, не уточняя, какой именно геометрии) я назову плоскость из связки, пересекающую сферу. Покажем теперь, что свойства точек и прямых в геометриях Римана, Лобачевского и Евклида – в точности отвечают трем возможным случаям расположения сферы S и точки О.
1. Точка О лежит внутри сферы S. в этом случае всякая прямая связки пересекает сферу в двух точках, значит, задает «точку» геометрии, а всякая плоскость связки – пересекает сферу по некоторой окружности и потому задает некоторую «прямую» геометрии.. Как было замечено, всякие две плоскости связки («прямые» нашей геометрии) пересекаются по некоторой прямой связки («точке» нашей геометрии). Значит в нашей геометрии – все прямые пересекаются, параллельных прямых нет. Это и происходит в геометрии Римана.
2. Точка О лежит вне сферы S. В этом случае не все прямые связки пересекают сферу и потому – не все задают «точку» геометрии. Прямые, пересекающие сферу, лежат внутри конуса с вершиной в О, а основание конуса – окружность на сфере S в точках которой прямые связки касаются S. Точно также – не все плоскости связки пересекают сферу и потому – не все задают «прямую» геометрии. Возьмем две произвольные плоскости, пересекающие сферу S. Они пересекаются по некоторой прямой связки. Если эта прямая не пересекает сферу S, то «прямые» геометрии, определенные плоскостями связки – не имеют «точки» пересечения в нашей геометрии. можно построить целое семейство непересекающихся «прямых» нашей геометрии. Возьмем прямую связки, не имеющую со сферой S общих точек. Проведем любые две плоскости, проходящие через эту прямую и пересекающие S. Все они задают «прямые» геометрии, не имеющие общих точек. Это свойство прямых характерно для геометрии Лобачевского.
3. Точка О лежит на сфере S. Этот случай занимает промежуточное положение между двумя рассмотренными. Здесь, как и в предыдущем варианте – есть прямые связки, не задающие ни одной «точки» геометрии. Все они лежат на плоскости Н, касающейся S в точке О. Плоскость Н – единственная плоскость связки не пересекающая S и потому – единственная, которая не определяет «прямой» геометрии. Как устроены непересекающиеся прямые в этой геометрии? Возьмем произвольную плоскость А связки, не совпадающую с Н. Она пересекается с Н по некоторой прямой L. Если другая плоскость связки, В пересекается с А по прямой L то «прямые» геометрии, заданные плоскостями связки А и В – не пересекаются. Предоставляю читателю самостоятельно проверить, что в этом случае выполняется пятый постулат Евклида, т.е. что через всякую точку геометрии всегда можно провести одну и только одну прямую не пересекающуюся с данной прямой.
Итак, мы видели, что свойства пересечений «прямых» геометрии, построенной на основе сферы S и связки с центром в О, в зависимости от расположения О вне, на поверхности, или внутри сферы S – соответствуют свойствам геометрии Лобачевского, Евклида или Римана. Теперь я покажу, как устроены осевые симметрии в этих геометриях. Для этого надо напомнить определение А-отображений в пространстве. Пусть дана произвольная точка В в пространстве, не лежащая на сфере S. А-отображением с центром в точке В сферы S называется отображение сферы в себя, при котором произвольной точке Х на сфере ставится в соответствие вторая точка пересечения прямой (В, Х) со сферой. Если (В, Х) касается сферы S , то В(Х)=Х (точка отображается сама в себя). Очевидна связь А-отображений с центром в В со связкой прямых с центром в точке В. Будем обозначать результат действия А-отображения с центром в точке В на Х как В(Х) (см. ст. 4). Очевидно из определения А-отображения В(В(Х))=Х. Иначе говоря В(Х) – инволютивное отображение и этим похоже на симметрию. поэтому А-отображения – хороший кандидат на симметрии геометрий, которые мы строим.
Ранее мы определяли «точку» геометрии как прямую связки с центром в О. Модифицируем определение. Назовем «точкой» геометрии – пару точек пересечения прямой связки со сферой. Или, такую пару точек на сфере S, которая лежит на одной прямой с О. Аналогично мы назовем «прямой» геометрии ту окружность, по которой плоскость связки пересекает сферу (или окружности сферы, лежащие в одной плоскости с О). После этой модификации мы можем изучать геометрию находясь на сфере S, а предыдущие определения годились, когда мы наблюдали сферу из точки О.
Произвольное А-отображение как-то отображает сферу S в себя. Чтобы А-отображение могло быть симметрией геометрии оно должно отображать «точки» геометрии снова в «точки» геометрии. Пусть В – центр А-отображения. Чтобы быть «кандидатом» в симметрии геометрии, В(Х) должно отображать пару точек, лежащую на одной прямой с О – снова в пару точек, лежащую на одной прямой с О. Запишем: если точки Х и Y на одной прямой с О, то В(Х) и B(Y) снова должны быть на одной прямой с О. (!) Заметим, что если О не на сфере S , то мы можем рассмотреть А-отображение с центром в О. То, что Х и Y лежат на одной прямой с О означает в точности то, что О(Х)=Y и условие (!) можно сформулировать и так: если О(Х)=Y, то О(В(Х))=В(Y). Или О(В(Х))=В(О(Х)). А это означает, что О(Х) и В(Х) – коммутируют. (см. начало ст. 4).
Пусть точка О, центр связки, лежит вне сферы S. Тогда, как было сказано ранее, на сфере S есть окружность, по которой прямые связки касаются S (основание конуса с вершиной в О). Эти касающиеся прямые связки не задают никакой точки геометрии. Более того, к точке К на этой окружности нельзя подобрать пару, т.е. вторую точку К1, такую, что (К, К1) – лежат на одной прямой с О и тогда пара точек (К, К1) задала бы точку геометрии. Легко понять, что все точки этой окружности должны остаться на ней же под действием А-отображений, подходящих для симметрий нашей геометрии, удовлетворяющих условию (!). Геометрически это означает, что все центры таких А-отображений должны лежать на плоскости, в которой лежит эта окружность касательного конуса. Эта плоскость называется полярой точки О. Пользуясь теорией поляр (см. ст. 4), можно доказать, что любая точка В на плоскости, полярной к О – удовлетворяет (!).
Итак, А-отображение с центром, лежащим на плоскости, полярной к О отображает точки геометрии (пары точек на сфере S, лежащих на одной прямой с О) в точки геометрии. Выясним, куда такое А-отображение отображает прямые нашей геометрии (окружности сферы, лежащие в одной плоскости с О). Не слишком сложно показать, что всякое А-отображение (где бы ни был его центр) отображает окружности сферы S – снова в окружности. (т.е. что если точки P, Q, T, W на сфере лежат на одной окружности, то и точки B(P), B(Q), B(T), B(W) – также лежат на одной окружности.) Для того, что А-отображение переводило «прямые» геометрии в «прямые» необходимо и достаточно, чтобы оно отображало всякую окружность, лежащую в одной плоскости с О в окружность, лежащую в одной в одной плоскости О. Опять-таки, я сошлюсь на теорию поляр. Впрочем есть и другие не слишком сложные способы доказать, что: если центр А-отображения лежит на поляре О, то требуемое выполняется. Поэтому А-отображения с центрами на поляре к О – отображают «точки» геометрии в точки геометрии, а «прямые» – в «прямые».
Заметим, что мы рассуждали, используя «окружность касательного конуса» с центром в точке О. Т.е. все наши рассуждения пригодны пока только для случая, когда точка О лежит вне сферы S. Теория поляр позволяет расширить доказанное и на случай, когда О лежит внутри или на сфере S. Если О лежит внутри S то существует плоскость, не пересекающая сферу, которую называют полярой О (она обладает тем свойством, что О лежит на поляре к каждой точке это плоскости). Если центр А-отображения лежит на ней – то все нужные нам свойства выполняются. (А если центр А-отображения не в этой плоскости, то А-отображение не переводит «точки» геометрии в «точки»). Если же О лежит на сфере S, то ее полярой называют плоскость, касающуюся S в О. Предоставляю читателю самостоятельно доказать, что А-отображения с центрами на этой плоскости переводят «прямые» геометрии в «прямые» и «точки» в «точки». Заметим еще, что, хотя в данном случае точка О не задает никакого А-отображения, мы можем все-таки связать с ней отображение, отображающее все точки сферы S в точку О. (О(Х)=О для всех Х на сфере). И тогда можно сказать, что В, центр А-отображения лежит на поляре к О тогда и только тогда когда О(Х) коммутирует с В(Х).
Также А-отображения сохраняют углы между «прямыми» геометрии. Ведь А-отображения это инверсия сферы S (действительная или мнимая см. ст. 4), а инверсия – сохраняет углы между окружностями. «прямые» геометрии это – частный случай окружностей, значит А-отображение сохраняет углы и между ними. Итак А-отображения:
1. Отображают прямые геометрии в прямые.
2. Сохраняют углы между ними.
3. Инволютивны А(А(Х))=Х
В случае геометрий Римана или Лобачевского уже первых двух условий достаточно для того, чтобы утверждать – А-отображения сохраняют расстояния между точками, являются движением плоскости. В случае геометрии Евклида подобие также сохраняет углы между прямыми, но оно не сохраняет расстояние между точками и потому не является движением геометрии. Но подобие – не инволютивно! С учетом п. 3 и в этом, Евклидовом случае А-отображение будет движением плоскости (евклидовой). Точнее говоря – симметрией.
Относительно чего симметрия? Пусть В – произвольная точка на поляре О, симметрию относительно чего задает А-отображение с центром в В? Если В – вне сферы, то А-отображение с центром в В определяет на S окружность касательного конуса с вершиной в В. Если точка сферы Х лежит на этой окружности, то В(Х)=Х. Из теории поляр известно, что эта окружность лежит в одной плоскости с О и потому – является «прямой» геометрии. Именно симметрию относительно этой прямой и задает А-отображение с центром в точке В. Если же В лежит на поляре О и находится внутри S, то рассмотрим прямую (В, О). Она пересекает сферу S в двух точках, эта пара точек определяет «точку» геометрии. Именно симметрию относительно этой «точки» геометрии и задает А-отображение с центром в точке В.
Укажем еще, что в случае, когда О лежит вне сферы S (случай геометрии Лобачевского), то сечение сферы S полярной к О плоскостью Н – даст известную модель Кэли-Клейна. «Точкой» в этой модели будет пересечение прямой связки, пересекающей сферу S с Н, а «прямой» – пересечение плоскости связки, пересекающей сферу, с Н.
На мой взгляд, приведенная модель разных геометрий симпатична и своей наглядностью и «однородностью» (разные геометрии получаются в результате простого перемещения точки О вне, на и внутрь поверхности сферы). Уже поэтому, думаю, их удобно использовать при обучении. Модель можно изучать и далее.

Окружности в разных геометриях.


Как, в рамках приведенной модели – выглядит окружность? Определим окружность немного необычно. Пусть дана точка Р – центр окружности и точка Q – лежащая на окружности. Окружностью я назову совокупность точек, в которую может перейти Q после симметрий, относительно всевозможных прямых, проходящих через Х.


Рассмотрим, что это означает для нашей модели. Точка Р изображается в нашей модели двумя точками Р1 и Р2, лежащими на одной прямой с О. А-отображения, оставляющие пару (Р1, Р2) неподвижной, это или:
1. А-отображения, центры которых лежат на прямой (Р1, Р2). Тогда точки Р1 и Р2 меняются местами.
2.А-отображения, центры которых лежат на плоскости, касающейся Р1 и на плоскости, касающейся Р2, т.е. – на пересечении этих плоскостей. Эти А-отображения отображают точку Р1 в Р1 и Р2 в Р2.
С другой стороны, нас интересуют только те А-отображения, которые лежат на Н, поляре О. Именно они определяют симметрии геометрии. Из теории поляр известно, что пара плоскостей, описанных в п.2 – пересекается по прямой, лежащей на Н, поляре О. Обозначим эту прямую L. Точка Q геометрии изображается на сфере парой точек Q1 и Q2 (лежащих на одной прямой с О). Проведем через L и Q1 плоскость, ее пересечение с S и даст совокупность точек на S, куда может перейти Q1 под действием А-отображений с центрами, лежащими на L. Пересечение сферы и плоскости это – окружность. Значит, окружность геометрии изображается окружностью на сфере (точнее, парой окружностей, ведь мы можем провести плоскость и через L и Q2). Заметим, что мы провели рассуждение, пригодное для всех трех случаев расположения S и О, т.е. для геометрий Римана, Лобачевского и Евклида одновременно. А случай, описанный в п. 1 отвечает точечной симметрии (относительно точки Р).
Чтобы не путаться в «парах точек» (изображающих точку геометрии), можно тем или иным удобным способом рассматривать часть сферы, в которой лежит по одному представителю пары. Например, если О – вне и выше сферы, то рассмотрим лишь ту часть сферы, которая лежит над полярой О, ближе к О.
У этой модели есть недостаток. Она – объемная. А мы изучаем плоские геометрии Римана, Евклида, Лобачевского. поэтому сейчас я дам плоскую модель, опять-таки однородно охватывающую все три случая.

Плоская модель различных геометрий.


Плоская модель начинается так просто, что это даже забавно. Возьмем любые три окружности А, В, С. Назовем их «прямыми» геометрии, а пары точек их пересечения – «точками» геометрии. Также, «прямыми» геометрии назовем все окружности, лежащие в образованных тремя исходными пучках. Пару точек пересечения из получающегося семейства – называем «точкой» геометрии, любую окружность, проходящую через эту пару точек – «прямой» геометрии, также любая окружность из пучка, заданного двумя окружностями из семейства – также будет «прямой» геометрии. (заметим, что именно окружности мы включаем в «прямые» геометрии, мнимые инверсии мы в данном случае не рассматриваем).
А какой геометрии? Это зависит от расположения исходных окружностей А, В, С. Если они – Римановы (т.е. одна из трех окружностей разделяет точки пересечения двух других), то и геометрия получается Римановой. Если А, В, С – евклидовы (т.е. все три пересекаются в одной точке, то и геометрия получится евклидовой. Если же А, В, С – три окружности Лобачевского (т.е. ни одна окружность не разделяет точек пересечения двух других), то и геометрия получится Лобачевского. (См. ст. 6 про окружность, ортогональную трем данным).
Прежде все разберем случай евклидового расположения трех окружностей А, В, С. Пусть О – точка, в которой они все пересекаются. Легко видеть, что всякая окружность из семейства, построенного указанным выше способом – проходит через О. (И, наоборот, всякую окружность, проходящую через О, можно получить из А, В, С описанным способом). Осуществим какую-нибудь инверсию с центром в О. При этом все окружности семейства («прямые» геометрии) перейдут в прямые обычной евклидовой плоскости. А «точки» геометрии – это пары точек (Х, О) где Х – любая точка плоскости. После инверсии О перейдет в бесконечно удаленную, а Х – в какую-то другую точку плоскости. Мы можем оперировать с этой парой как с одной точкой, ведь вторая точка во всех парах – одинакова и бесконечно далека. Мы получили обычную Евклидову геометрию.
Какие окружности, пересекающиеся в О, изображают параллельные прямые? Т.к. у параллельных прямых нет точки пересечения (кроме бесконечно удаленной, а ее-то и изображает точка О), то и у таких окружностей О должна быть единственной общей точкой. Это возможно только если они касаются друг друга в точке О. Итак – параллельные прямые изображаются касающимися в точке О окружностями.
Заметим, что А(О)=В(О)=С(О) и любая окружность, проходящая через О – оставляет О неподвижной при инверсии. Поэтому никакой композицией инверсий невозможно отобразить какую-нибудь другую точку Х в точку О. Это – тоже свойство бесконечно удаленной точки. Никаким движением нельзя в нее попасть и она неподвижна при всех движениях плоскости.
В случае риманова расположения трех исходных А, В, С – любые две окружности, изображающие «прямые» геометрии пересекаются, так ведут себя прямые римановой геометрии. Если же исходные А, В, С – окружности Лобачевского, то среди окружностей, изображающих «прямые» геометрии есть очень много непересекающихся, что свойственно геометрии Лобачевского. Теперь заметим, что в случаях Риманова или Лобачевского расположения трех исходных окружностей А, В, С – существует ортогональная всем троим инверсия I. В случае Лобачевского I – действительная инверсия, у которой есть неподвижная окружность, в случае Риманова расположения исходных А, В, С – I будет мнимой инверсией. Все окружности, полученные описанным способом, изображающие «прямые» геометрии – будут ортогональны I. Это следует из того, что все окружности из пучков (A, B), (В, С), (А, С) – будут Ортогональны I, т.к. I ортогональна А, В, С, а пары точек пересечения окружностей, изображающих «прямые» – сопряжены относительно I. (см. ст. 6 и ст. 2).
Если радиус окружности I очень мал или мы расположены очень далеко от этой окружности, то свойства геометрий Лобачевского и Римана будут похожи на свойства геометрии Евклида. Ведь «очень маленькая окружность» – это почти точка. Или, если далеко уйти от окружности – она тоже покажется точкой.

Связь плоской и пространственной моделей.


Свяжем эту модель с построенной ранее пространственной моделью. Пространственная модель, коротко говоря, сводится к тому, что выбирается А-отображение с центром в О сферы S. Затем рассматривается совокупность А отображений, коммутирующих с О(Х), они лежат на поляре к О. Но А отображения – это инверсии сферы. Выбрать А-отображение с центром в О – означает просто выбрать инверсию, а А-отображения, коммутирующие с этой инверсией – есть инверсии, коммутирующие с исходной, определенной точкой О. поэтому две модели равносильны. Это стало бы совсем очевидно, если бы я начал построение плоской модели так: «назовем окружности, ортогональные данной инверсии I – «прямыми» геометрии. Если I – мнимая инверсия, то это геометрия Римана, а если I – действительная, то получится геометрия Лобачевского.»Этот способ был бы хуже по двум причинам: 1. Выпадает геометрия Евклида. 2. окружность I совершенно не нужна нам для доказательства многих теорем.
Как и в пространственной модели я рассмотрю, что будет являться окружностью в рамках предложенной модели. Для этого снова воспользуемся определением окружности, данным на рис. 1. «Прямые» геометрии, проходящие через «точку» Р геометрии – это окружности, проходящие через пару точек Р1 и Р2, мы ищем как действуют инверсии относительно всех этих окружностей на «точку» геометрии. «точка» геометрии это пара точек Q1 и Q2, но нам вполне достаточно проследить действие на одну из этих точек, например Q1.


Окружности, проходящие через Р1 и Р2 образуют пучок. Проведем через Q1 окружность Т, ортогональную каким-нибудь двум окружностям этого пучка, напр. исходным F и Н, по свойствам пучков – она будет ортогональна все окружностям пучка (F, H) и, следовательно, при инверсиях относительно окружностей и пучка точка Q1 будет перемещаться по окружности Т. Таким образом, окружность геометрии изображается окружностью на плоскости. Заметим, что наше рассуждение охватывает сразу три возможные случая (Римана, Евклида и Лобачевского)
Но, в случае геометрии Лобачевского – не всякая окружность на плоскости будет окружностью геометрии Лобачевского. Пусть две окружности, изображающие «прямые» геометрии Лобачевского не пересекаются.


Окружность Т, ортогональная F и Н не изображает никакой окружности геометрии Лобачевского, т.к. у нее нет «центра» в этой геометрии. Заметим, что центры мнимого пучка (F, H) О1 и О2 лежат на I – окружности, ортогональной всем окружностям, изображающим «прямые» геометрии Лобачевского. Т.к. Т проходит через О1 и О2, то Т – обязательно пересекает I – именно такие окружности – не изображают никакую окружность геометрии Лобачевского.
Заметим еще одно хорошее свойство этой модели: угол между окружностями, изображающими «прямые» геометрии совпадает с углом между прямыми, которые эти окружности изображают.

Плодотворность плоской модели.


На мой взгляд эта плоская модель весьма удобна для доказательств теорем всех геометрий: Римана Евклида, Лобачевского. Особенно модель плодотворна для доказательств теорем о треугольниках – это сводится к доказательству каких-то свойств трех окружностей А, В, С.
Заметим, что расстояние между «точками» геометрий нужно изучать и определять специально (на основании гармонического отношения, ст. 4, 5), а вот углы между «прямыми» – это просто углы между изображающими их окружностями. Поэтому и теоремы проще доказывать про углы, биссектрисы и т.п. Приведу два примера:
1. Сумма углов треугольника в разных геометриях.
2. Биссектрисы треугольника пересекаются в одной точке во всех трех геометриях.

Сумма углов треугольника или «углы в трехокружнике».


В геометрии Евклида.


Вершинами Евклидова треугольника будут вторые точки пересечения окружностей А, В, С между собой (первую, точку О – можно отбросить, т.к. в ней пересекаются все прямые и изображающие их окружности). Треугольник PQH изображен в модели тремя дугами PQ, QH, и HP. Теперь воспользуемся тем, что окружности пересекаются в двух точках и углы – одинаковы в обеих точках. Мы видим, что углы между соответствующими дугами – сходятся в точке О и там дополняют друг друга (без пересечений) до угла в 180 градусов. следовательно, сумма углов между указанными дугами равна 180 градусов и сумма углов треугольника также. Что и требовалось. Заметим, что это доказательство не требует проведения каких-либо вспомогательных линий. А при обычном доказательстве надо провести прямую через одну из вершин, параллельную третьей стороне.
В геометрии Римана сумма углов треугольника всегда больше 180 градусов.


Проведем три римановы окружности А, В, С. В качестве сторон треугольника возьмем дуги, ограничивающие область, лежащую внутри всех окружностей. Проведем окружность D через не входящую в треугольник точку пересечения А и В и две точки пересечения С с А и С с В. Точки пересечения возьмем входящие в треугольник. Окружности А, В, D – пересекаются в одной точке, значит, по доказанному ранее – сумма их углов равна 180 градусов. Но окружность D входит внутрь дуг, образующих треугольник и проходит через его вершины, поэтому сумма углов между D, B, A всегда меньше, чем сумма углов между А, В, С, поэтому сумма углов, образованных дугами АВ, ВС и СА – больше 180 градусов. что и требовалось. (По-моему это рассуждение практически невозможно понять без чертежа, но даже на плохом рисунке оно довольно прозрачно, главное не ошибиться с ориентацией углов и не запутаться в основном и дополнительном угле).
В геометрии Лобачевского сумма углов треугольника всегда меньше 180 градусов.


В этом случае мы считаем треугольником три точки пересечения А, В, С между собой, которые лежат дальше от той точки пересечения А и С, через которую проходит D. В этом случае D не зайдет в треугольник, хотя и пройдет через две его вершины. Поэтому сумма углов трехокружника А. В, С меньше суммы углов трехокружника А, В, D, а последняя равна 180 градусов, т.к. A, B, D – пересекаются в одной точке. Как и в прошлом случае – рассуждение очень прозрачно даже на плохом чертеже.
В случае Римана или Лобачевского есть проблема выбора трех точек, которые можно рассматривать как вершины треугольника. Также не ясно, какие дуги нужно считать сторонами. Эта проблема сводится к такой: точка геометрии изображается парой точек пересечения окружностей. Как выбрать из этой пары одну точку? Для этого удобно привлечь окружность I, ортогональную А, В, С. Если I – действительная окружность и мы имеем дело с геометрией Лобачевского, то пара сопряженных относительно нее точек – разделяется этой окружностью. Мы можем выбрать в качестве представителя – точку пары, лежащую внутри окружности I. Тогда все точки геометрии – это точки внутри окружности I. Если же I – мнимая инверсия, то мы можем выбрать какую-нибудь действительную окружность, ортогональную I. под действием I эта окружность «вывернется наизнанку», она разделяет сопряженные относительно I точки и мы опять-таки можем выбрать в качестве точек геометрии – внутренность этой окружности. Впрочем не во всех теоремах есть необходимость этим пользоваться.
Заметим, что хотя теоремы становится проще доказывать из-за того, что окружности пересекаются в двух точках и это увеличивает количество равных углов, надо быть и внимательней, т.к. надо учитывать ориентацию углов, различать прямой и дополнительный углы.

Изогональные окружности.


Прежде, чем доказывать теорему о биссектрисах изучим свойства «изогональных окружностей».
Пусть даны две окружности А и В. Окружность С называется изогональной к А и В если угол между А и С равен углу между В и С. Частный случай изогональных окружностей – когда С касается А и В или когда С – ортогональна А и В. Рассмотрение изогональных окружностей приучает нас внимательно относиться к расположению углов и замечать их ориентацию. Мы докажем, что все окружности, изогональные к двум данным А и В – распадаются на два семейства. Одно семейство – ортогонально одной биссектрисе между А и В, другое – другой биссектрисе. Окружности, ортогональные А и В принадлежат обеим семействам сразу. Если же А и В касаются, то у них всего одна биссектриса. Изогональные к ним окружности также распадаются на два семейства. Одно – ортогонально единственной биссектрисе, а другое – все окружности, проходящие через точку касания А и В. Опять-таки – окружности, ортогональные А и В лежат в обеих этих семействах одновременно.
То, что окружности из этих семейств изогональны к А и В доказывается тривиально. Пусть I – какая-то биссектриса между А и В, I(A)=B. Пусть С – ортогональна I, I(C)=C, тогда угол между А и С равен углу между I(A)=B и I(C)=C, т.е. равен углу между В и С, что и требовалось. Если же А и В касаются и С проходит через точку касания А и В:


Всякая окружность С, проходящая через Р пересекает А и В под тем же углом, что и их общую касательную прямую. Это аналогично тому, что всякая прямая пересекает пару параллельных прямых под одним углом. что и требовалось.
Нам осталось доказать, что всякая окружность, изогональная к двум данным А и В – принадлежит к одному из описанных семейств. Сначала рассмотрим случай, когда А и В – не касаются. Заметим, что нам достаточно доказать, что на всякой изогональной к А и В окружности С есть пара точек, сопряженных друг с другом относительно какой-то биссектрисы между А и В.
Сначала заметим, что если С касается А и В, то всякая окружность, проходящая через точки касания – изогональна к А и В.


Т.к. С и А касаются то С1 изогональна к С и А, т.к. С и В касаются, то С1 изогональна к С и В. Значит С1 изогональна к А и В. Что и требовалось. Приведем другое доказательство. В ст. 3 было доказано, что касающиеся А и В окружности ортогональны одной из биссектрис между А и В, точки касания сопряжены относительно этой биссектрисы, следовательно С1, проходящая через эти точки касания будет ортогональна этой биссектрисе. А мы только что доказали, что окружности, ортогональные биссектрисе между А и В – изогональны к А и В. что и требовалось.

Ориентация и расположение углов.


Прежде чем двинуться дальше, необходимо заметить простые свойства ориентации (расположения) углов. Начнем с геометрии прямых. Пусть есть три прямые Н, Т, К пересекающиеся в точке О и мы знаем, чему равны углы между Н1 и Т и между Т1 и К. Тогда угол между Н1 и К равен или сумме или разности этих углов, в зависимости от их ориентации. Ориентацией я называю направление вращения точки О при движении от одной прямой к другой по известному углу. Точно также обстоит дело и с тремя окружностями, пересекающимися в одной точке. Но, в геометрии окружностей есть феномен, которого нет в геометрии прямых. у двух окружностей Н и Т – есть вторая точка пересечения. И, если мы рассмотрим ориентацию того же угла между Н и Т во второй точке пересечения – они будет противоположна ориентации в первой точке пересечения!


Т.е. точки вблизи О будут вращаться в одну сторону, а вблизи О1 – в другую. Разумеется, есть и переходный случай – когда эти точки движутся по прямой, а у прямой – нет ориентации! поэтому в случае окружностей, говоря про ориентацию угла между окружностями нужно добавлять – в какой точке пересечения мы ее определяем. Заметим еще одно. Если угол между Н и Т равен 90 градусов (Н и Т ортогональны), то нет возможности говорить об ориентации угла. Ведь этот угол равен своему дополнительному.
Вернемся к изогональным окружностям. Пусть окружность С изогональная А и В пересекает окружность А и в точках А1 и А2, окружность В в точках В1 и В2. Мы докажем сейчас, что С – ортогональна какой-нибудь биссектрисе между А и В. Не будем пока интересоваться точкой А2. Рассмотрим ориентацию угла между А и С в точке А1 и ориентации равных ему по величине углов между В и С в точках В1 и В2. Поскольку последние две ориентации – противоположны друг другу, то одна из них совпадает с ориентацией угла между А и С в точке А1, а другая – противоположна. Выберем из точек В1 и В2 ту, в которой ориентация угла между В и С противоположна ориентации угла между А и С в точке А1. Пусть это точка В1.
Проведем через А1 и В1 произвольную окружность D и покажем что она – всегда изогональна к А и В.


Рассмотрим углы между А и D , D и С и между А и С и их ориентации в точке А1. Пусть например, ориентация угла между С и D та же что и между А и С. Тогда угол между А и D равен их сумме. Теперь рассмотрим углы и их ориентации в точке В1. Угол между В и С, по выбору точки В1 имеет ориентацию противоположную ориентации угла между А и С, угол между С и D имеет ориентацию, противоположную той, что имеет в точке А1 (т.к. окружности С и D пересекаются в точках А1 и В1 и ориентации этого угла противоположны в этих точках). Значит угол между В и D равен углов между В и С и между С и D. Т.к. угол между В и С равен углу между А и С то из приведенного следует, что угол между А и D равен углу между В и D. Что и требовалось.
Если же ориентация угла между С и D противоположна в точке А1 ориентации в этой же точке угла между А и С, то угол между А и D равен разности угла между А и С и угла между С и D. В точке В1 соответствующие ориентации – обе изменятся на противоположные и поэтому останутся противоположны друг другу. Угол между В и D поэтому будет равен разности между углами В с D и С с D. Отсюда опять-таки получим, что угол между B и D равен углу между А и D. Что и требовалось. Теперь проведем через точки А1 и В1 окружность D1, касающуюся А в точке А1. По доказанному D1 образует с В тот же угол, что и с А, т.е. – касается окружности В в точке В1. Мы уже доказали (ст. 3), что окружность, касающаяся А и В ортогональна какой-то их биссектрисе, и что точки их касания – сопряжены относительно этой биссектрисы. Следовательно А1 и В1 сопряжены относительно какой-то биссектрисы между А и В, и все окружности, проходящие через эти точки – ортогональны этой биссектрисе, следовательно – окружность С тоже ей ортогональна. Что и требовалось.
Если А и В касаются и С изогональна им, то, если с не проходит через общую точку касания все наши рассуждения переносятся без ущерба. (с небольшими модификациями). Итак, мы доказали, что окружности, изогональные двум данным – ортогональны одной из биссектрис или (если данные окружности касаются) – проходят через точку их касания.

Теорема о пересечении биссектрис трех окружностей и неевклидовы геометрии.


Пусть даны три произвольные, не касающиеся друг друга окружности и D1 – какая-то биссектриса между А и В, а D2 – какая-то биссектриса между В и С. Теорема утверждает, что одна из двух существующих биссектрис между А и С обязательно лежит в пучке, образованном D1 и D2. Доказательство.
Рассмотрим пучок окружностей, ортогональных D1 и D2. Все окружности этого пучка изогональны и к А и В и к В и С. в самом деле, пусть О – какая-то окружность этого пучка. D1(O)=O, D1(A)=B следовательно угол между О и А равен углу между О и В. D2(O)=O, D2(B)=C, следовательно угол между О и В равен углу между О и С. Из этих равенств следует, что угол между О и А равен углу между О и С (транзитивность равенства). Это означает, что О изогональна и к А и С. Из доказанного следует, что О – ортогональна какой-то биссектрисе между А и С. Проведем еще О1 и О2 из пучка, ортогонального к D1 и D2, каждая из них изогональна к А и С и потому будет ортогональна какой-то биссектрисе между А и С. Т.к. из трех окружностей О, О1, О2 – каждая ортогональна одной из двух биссектрис между А и С, следовательно какая-то из биссектрис между А и С ортогональна двум из этих трех окружностей, следовательно, эта биссектриса лежит в том же пучке, что D1 и D2. Что и требовалось. Предоставляю читателю самостоятельно разобрать случай, когда среди А, В, С – есть касающиеся окружности.
Вернемся к нашей модели разных геометрий. Согласно ей, три окружности А, В, С – прямые (неизвестно какой геометрии, Римана, Лобачевского или Евклида). Тем самым мы доказали, что в любом треугольнике – любой геометрии – биссектрисы пересекаются. Правда, требуется установить, какие именно биссектрисы!
Ранее доказав, что изогональные окружности ортогональны биссектрисе, мы доказали в терминах нашей модели (любой геометрии!), что в треугольнике, углы при одной из сторон которого равны – биссектриса противоположного угла ортогональна этой стороне. Правда, и здесь требуется уточнить, какие именно углы равны.
Итак, мы видим, что предложенная модель позволяет вполне эффективно доказывать теоремы неевклидовых (и евклидовой) геометрий одновременно.
Используются технологии uCoz